As we have already covered two algorithms those are Bubble Sort algorithm and Insertion Sort along with their implementation. In this blog we are covering Merge Sort Algorithm along with its complexity, how this algorithm actually works. With the Merge Sort Algorithm we will compare all other algorithms to check their time complexities and space complexities. Let’s explore this algorithm and understand how everything will go with the process and its working.
What is Merge Sort Algorithm?
The Merge Sort Algorithm is a classic divide and conquer sorting technique used in computer science to arrange elements in a specific order typically ascending or descending. It works by recursively breaking down a list into smaller sublists until each sublist contains a single element and then merging those sublists in a manner that results in a sorted list.
Here’s how the merge sort algorithm works step by step –
- Divide: Split the array into two halves.
- Conquer: Recursively sort each half using merge sort.
- Combine: Merge the two sorted halves into one sorted array.
Example:
Consider an unsorted array: [38, 27, 43, 3, 9, 82, 10]
- First it will split into [38, 27, 43] and [3, 9, 82, 10]
- Each part is further divided and sorted individually.
- Finally, the sorted subarrays are merged to form [3, 9, 10, 27, 38, 43, 82]
Key Features of Merge Sort Algorithm
- Time Complexity: O(n log n) in the worst, average, and best case.
- Space Complexity: O(n) due to the temporary arrays used during merging.
- Stable Sort: It preserves the relative order of equal elements.
- Not In Place: Requires additional memory for merging.
The merge sort algorithm is especially useful for large datasets where a stable and predictable time complexity is crucial.
How Merge Sort Works?
To understand how the merge sort algorithm works, imagine splitting a problem into smaller parts, solving each part, and then combining the solutions. That is the essence of the merge sort technique.
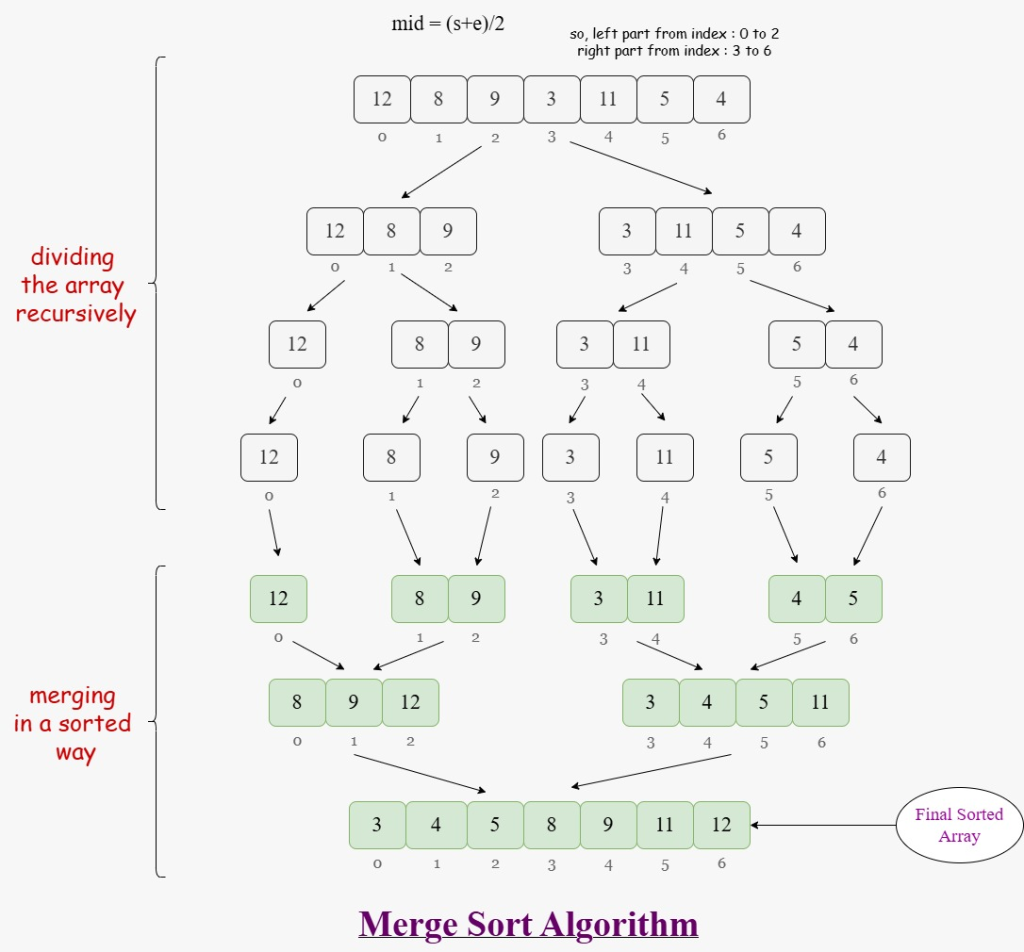
Here is a step by step breakdown of how the merge sort algorithm works –
Divide the Array
The array is recursively divided into two halves until each sub-array contains only a single element (or is empty). At this stage, every sub-array is trivially sorted.
Conquer by Sorting
Once the array is divided down to single elements, the merge sort algorithm begins to merge the sub-arrays. But instead of simply combining them, it compares the elements and sorts them during the merging process.
Combine by Merging
Two sorted sub-arrays are merged into one sorted array. This merging continues up the recursive chain until the entire array is reassembled in sorted order.
Merge Sort Algorithm Implementation in Python
def merge_sort(arr):
if len(arr) > 1:
# Finding the middle of the array
mid = len(arr) // 2
# Dividing the array elements into 2 halves
left_half = arr[:mid]
right_half = arr[mid:]
# Recursively sort both halves
merge_sort(left_half)
merge_sort(right_half)
# Merging the sorted halves
i = j = k = 0
# Copy data to temp arrays left_half[] and right_half[]
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1
# Checking if any element was left in left_half
while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1
# Checking if any element was left in right_half
while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1
# Example usage
sample_array = [38, 27, 43, 3, 9, 82, 10]
print("Original array:", sample_array)
merge_sort(sample_array)
print("Sorted array:", sample_array)
Example of Merge Sort Algorithm
We are Choosing array [19, 7, 18, 9, 4, 7, 14, 9] and with this array we are performing merge sort algorithm
Step 1: Divide the array
Split the array into halves until each sub-array contains a single element.
[19, 7, 18, 9, 4, 7, 14, 9]
→ [19, 7, 18, 9] and [4, 7, 14, 9]
→ [19, 7], [18, 9], [4, 7], [14, 9]
→ [19] [7] [18] [9] [4] [7] [14] [9] (Splitted the complete array in sub arrays)
Step 2: Merge and sort the smaller arrays
Start merging while sorting:
- [19] + [7] → [7, 19]
- [18] + [9] → [9, 18]
- [4] + [7] → [4, 7]
- [14] + [9] → [9, 14]
Now merge again this –
- [7, 19] + [9, 18] → [7, 9, 18, 19]
- [4, 7] + [9, 14] → [4, 7, 9, 14]
Step 3: Final Merge
- [7, 9, 18, 19] + [4, 7, 9, 14]
→ Compare and merge:
→ [4, 7, 7, 9, 9, 14, 18, 19] - Final Sorted Output
4 7 7 9 9 14 18 19
Merge Sort without Recursion
Merge Sort is a method used to sort numbers by dividing the list into smaller parts and then combining them in the right order. In the non-recursive or iterative version and we start by treating each number as a small sorted list. Then we keep merging pairs of these small lists step by step until the whole list is sorted. This process is repeated by doubling the size of the parts each time. It is a simple and efficient way to sort as even for large lists.
def merge(left, right):
result = []
i = j = 0
# Merge the two sorted halves
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# Add remaining elements (if any)
result.extend(left[i:])
result.extend(right[j:])
return result
def merge_sort_iterative(arr):
n = len(arr)
width = 1
# Iteratively merge subarrays of increasing size
while width < n:
for i in range(0, n, 2 * width):
left = arr[i:i + width]
right = arr[i + width:i + 2 * width]
arr[i:i + 2 * width] = merge(left, right)
width *= 2
return arr
# Example usage
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort_iterative(arr)
print("Sorted array:", sorted_arr)
Advantages of Merge Sort Algorithm
- It always gives the correct sorted result no matter how the input looks.
- It is fast and efficient even for large amounts of data.
- It does not get worse with messy input like some other sorting methods.
- It works well with linked list data structure because of how it divides and merges.
- It keeps equal items in the same order as it is a stable sort algorithm.
Disadvantages of Merge Sort Algorithm
- It uses more memory because it needs extra space to merge arrays.
- It can be slower than other sorts like quick sort for small datasets.
- It does a lot of splitting and merging which can feel like extra work.
- It is not the best choice for low memory devices due to space usage.
- It does not sort in place meaning it copies data instead of sorting where it is