In machine learning we often use linear regression to make predictions based on data. But sometimes the model learns the training data too well including the noise or errors. This is called overfitting and it makes the model perform badly on new data.
To solve this problem we use a method called regularization. It helps control how much the model depends on each feature. Two common types of regularization are called Ridge and Lasso Regression.
Ridge and Lasso Regression are better versions of linear regression. They add a penalty to the model to keep it simple and prevent overfitting. Ridge Regression makes all feature weights smaller but keeps them in the model. Lasso Regression can remove the unimportant ones by making their weights zero. In this blog you will learn about ridge and lasso regression in Python and see how to use them with examples.
What are Ridge and Lasso Regression?
Ridge regression and Lasso regression are techniques used to improve linear regression models by preventing overfitting. Ridge regression works by adding a penalty to the size of the coefficients, shrinking them towards zero but never exactly zero, which helps when factors are related. Lasso regression also adds a penalty but can shrink some coefficients exactly to zero, effectively selecting only the most important features. Both methods help create simpler, more reliable models that perform better on new data.
Understanding Regularization in Machine learning
Before we dive deeper into ridge and lasso regression in Python it’s important to understand what regularization means in machine learning.
When we train a machine learning model our goal is to make it perform well not just on the training data but also on new data it has never seen before. However sometimes the model fits the training data too perfectly. It learns even the random noise or patterns that do not really matter. This is known as overfitting and it leads to poor performance on real-world data.
Regularization helps fix this by adding a rule that keeps the model simple. It does this by reducing the size of the weights or coefficients in the model. Smaller weights usually mean the model is less sensitive to noise and more general in its predictions. Ridge and Lasso Regression are two regularization techniques that work by adding this extra rule to the model’s training process.
What is Ridge Regression (L2 Regularization)?
Ridge Regression is a type of linear regression that uses something called L2 regularization. This means it adds a penalty to the model when the weights or coefficients become too large. The idea is to keep the model simple so it does not overfit the training data.
In ridge regression we still try to find the best line or curve that fits the data. But while doing that we also make sure that the values of the coefficients stay small. This is done by adding the square of the coefficients to the loss function the model is trying to minimize.
Ridge regression is helpful when we have many features and some of them are related to each other. Instead of removing features it keeps all of them and just reduces their impact. This makes ridge regression a good choice when we want to keep all our input variables but still control overfitting.
What is Lasso Regression (L1 Regularization)?
Lasso Regression is another version of linear regression that uses L1 regularization. Just like ridge regression it tries to prevent overfitting by adding a penalty to the model. But the way it does this is a little different.
In lasso regression the penalty is based on the absolute values of the coefficients instead of their squares. This small change makes a big difference. It allows lasso regression to make some of the coefficients exactly zero. This means it can completely remove some features from the model.
Lasso regression is useful when we think that only a few features are important and the rest can be ignored. It helps us find the most useful features and build a simpler model. If we have a lot of input variables and we want to do feature selection then lasso regression is a good choice.
Ridge vs Lasso Regression: Key Differences
| Feature | Ridge Regression | Lasso Regression |
| Regularization Type | L2 Regularization | L1 Regularization |
| Penalty Term | Sum of squares of coefficients | Sum of absolute values of coefficients |
| Effect on Coefficients | Shrinks them close to zero | Can make some coefficients exactly zero |
| Feature Selection | Does not perform feature selection | Performs automatic feature selection |
| When to Use | When all features are important | When only some features are important |
| Multicollinearity Handling | Works well with multicollinearity | May arbitrarily select one of the features |
| Model Complexity | Keeps all features with smaller weights | Results in a simpler and more sparse model |
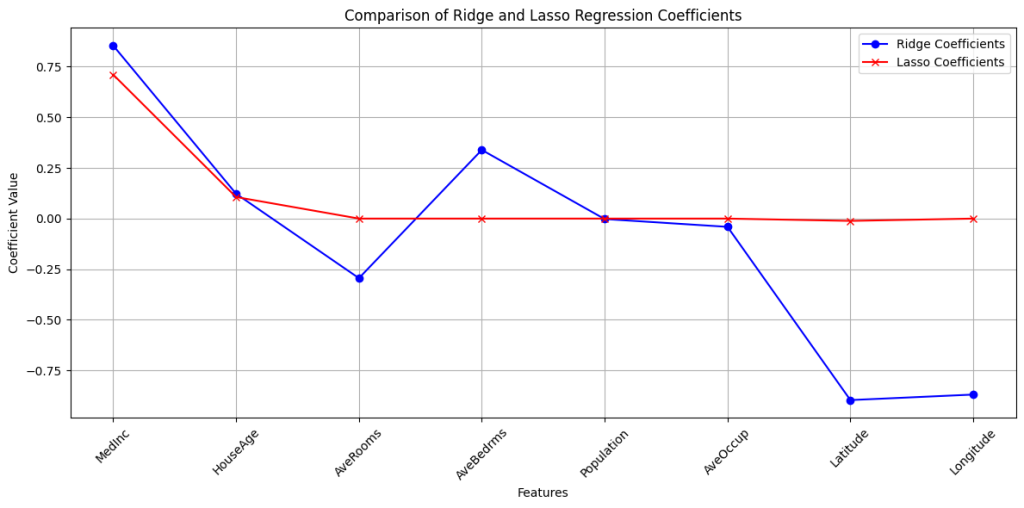
Implementing Ridge and Lasso in Python
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import Ridge, Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import plotly.graph_objects as go
data = fetch_california_housing()
X = data.data
y = data.target
feature_names = data.feature_names
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
ridge = Ridge(alpha=1.0)
lasso = Lasso(alpha=0.1)
ridge.fit(X_train_scaled, y_train)
lasso.fit(X_train_scaled, y_train)
ridge_coef = ridge.coef_
lasso_coef = lasso.coef_
df = pd.DataFrame({
'Feature': feature_names,
'Ridge Coefficient': ridge_coef,
'Lasso Coefficient': lasso_coef
})
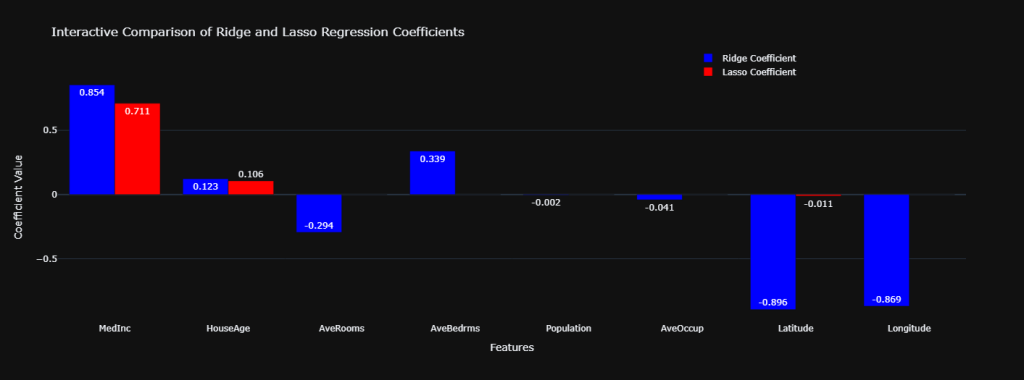
fig = go.Figure()
fig.add_trace(go.Bar(
x=df['Feature'],
y=df['Ridge Coefficient'],
name='Ridge Coefficient',
marker_color='blue',
text=df['Ridge Coefficient'].round(3),
textposition='auto',
hovertemplate='Feature: %{x}<br>Ridge Coef: %{y:.4f}<extra></extra>'
))
fig.add_trace(go.Bar(
x=df['Feature'],
y=df['Lasso Coefficient'],
name='Lasso Coefficient',
marker_color='red',
text=df['Lasso Coefficient'].round(3),
textposition='auto',
hovertemplate='Feature: %{x}<br>Lasso Coef: %{y:.4f}<extra></extra>'
))
fig.update_layout(
title='Interactive Comparison of Ridge and Lasso Regression Coefficients',
xaxis_title='Features',
yaxis_title='Coefficient Value',
barmode='group',
template='plotly_dark',
legend=dict(x=0.7, y=1.1, bgcolor='rgba(0,0,0,0)'),
hovermode='x unified'
)
fig.show()
Conclusion
Ridge and Lasso regression are two ways to help machine learning models do better by stopping them from getting confused by too much data Ridge tries to keep all features but makes them smaller while Lasso can ignore some features completely by making their effect zero Both are useful depending on your data and what you want to achieve Using Python you can easily try both methods and see which one works best for your problem.
Frequently Asked Questions
What is the main purpose of Ridge and Lasso regression?
Both help to prevent overfitting in machine learning models by adding a penalty to the size of coefficients
How is Ridge regression different from Lasso regression?
Ridge regression shrinks coefficients but keeps all features while Lasso regression can set some coefficients exactly to zero which means it removes less important features.
When should I use Ridge regression?
Use Ridge when you think all features are important but want to reduce their impact to avoid overfitting.
When should I use Lasso regression?
Use Lasso when you want to do feature selection by ignoring irrelevant features in your model.
Can I use both Ridge and Lasso together?
Yes combining them leads to Elastic Net regression which balances both penalties and works well in many cases.