When you write a program or solve a problem then you want to know how fast or efficient your solution is. That’s where asymptotic analysis in data structure comes in a picture. This concept really helps you to understand the performance or working of your algorithm when you are giving input size and that is really huge.
Instead of using actual time, we are using mathematical concepts to analyze the problems and to describe how our algorithm performs with the given input size. In this blog we will be covering the introduction to asymptotic analysis, discuss different types of asymptotic notations as those are Big-O, Big-Theta and Big-Omega notations.
What is Asymptotic Analysis?
Asymptotic analysis is a method used in computer science to describe the efficiency of an algorithm as the input size grows. It helps us understand how an algorithm behaves when it’s given a very large amount of data, without worrying about the specific hardware or the exact execution time.
Instead of measuring time in seconds, asymptotic analysis focuses on how the number of operations grows. It gives us a high level view of an algorithm’s performance.
Why is Asymptotic Analysis Important?
- Platform Independence – It does not matter if you are running the algorithm on a supercomputer or a laptop. Asymptotic analysis gives a general idea of performance that does not depend on machines.
- Comparison Tool – It allows us to compare algorithms purely based on efficiency. For example should you use Merge Sort or Bubble Sort? Asymptotic analysis helps you decide in your problem.
- Scalability Insight – It helps predict how the algorithm will perform with large datasets that is essential in real world applications like search engines big data or AI.
- Optimization Guidance – Helps developers spot inefficiencies in algorithms and improve performance especially in applications dealing with large data.
- Interview Readiness – Understanding asymptotic behavior is key to solving algorithm based questions in coding interviews and competitive programming.
Types of Asymptotic Notations
There are different types of Asymptotic notations which includes Big-O notation, Big-Theta notation and Big-Omega notations. Let’s discuss each one by one.
Big-O Notation
Big-O notation represents the maximum time that an algorithm can take. It is used basically when you want to be ready for the worst case scenario.
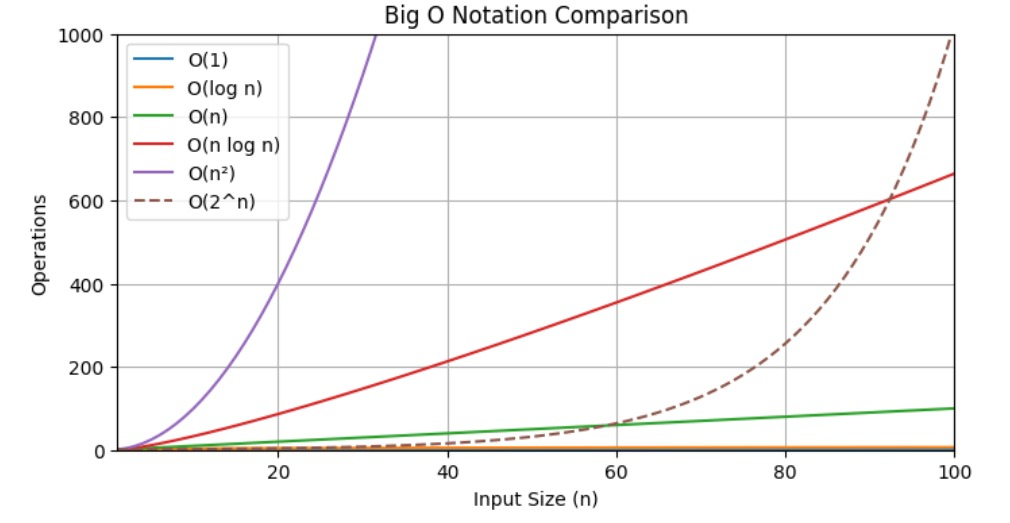
Example : Linear Search = O(n) whereas for Binary Search = O(logn) that represents if your algorithm is O(n) then it means if you give it 1 million items then it will go through them one by one.
Big-Theta Notation
This approach or notation is used when best and worst cases are close and wants to give a balanced view. Example : For an algorithm that always takes similar time is Θ(n).
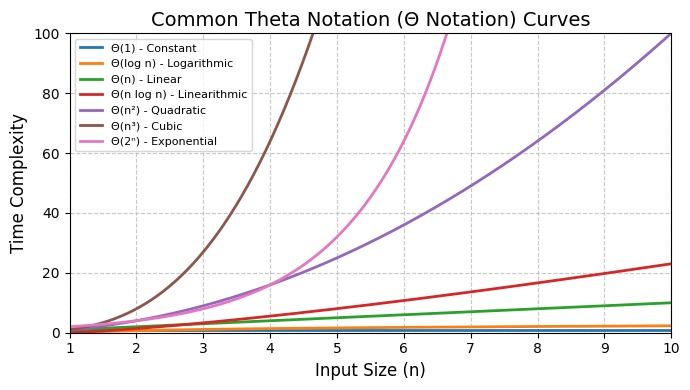
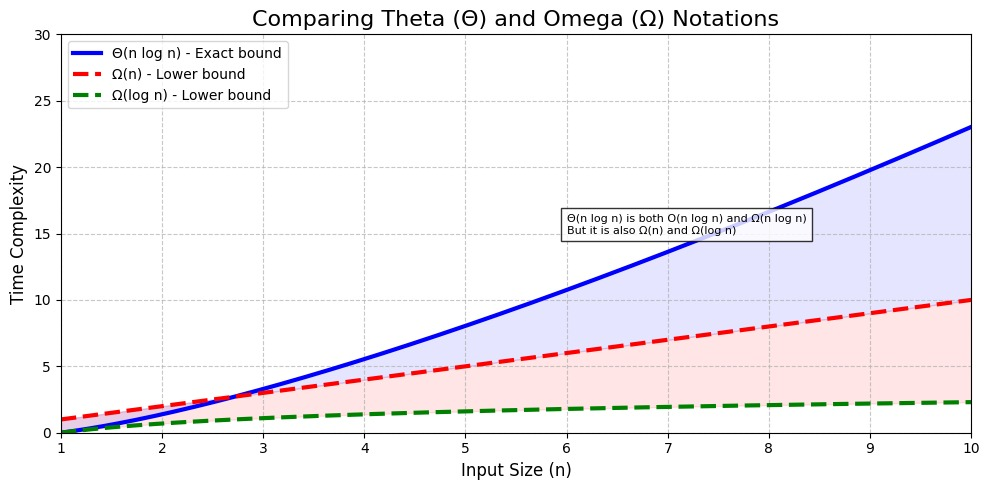
Big-Omega Notation
It tells the least time an algorithm will take. Not very useful alone but helps to complete the picture. Example : Linear Search → Ω(1) when target is first element.
Comparison of Common Algorithms
| Algorithm | Best Case | Average Case | Worst Case |
| Linear Search | Ω(1) | Θ(n) | O(n) |
| Binary Search | Ω(1) | Θ(log n) | O(log n) |
| Bubble Sort | Ω(n) | Θ(n²) | O(n²) |
| Merge Sort | Ω(n log n) | Θ(n log n) | O(n log n) |
| Quick Sort | Ω(n log n) | Θ(n log n) | O(n²) |
Visualizing Big-O Asymptotic Notation
This diagram given below helps you to visualize the big-O notation and through different input sizes.
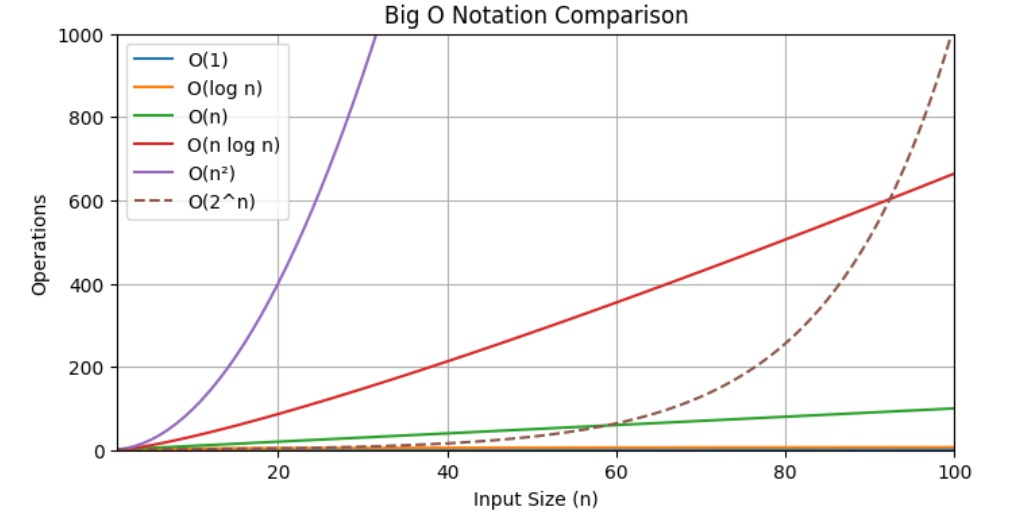
Real Life Examples of Asymptotic Analysis
Let’s say if you are searching for a friend’s name in a contact list.
- O(n): You check every name one by one.
- O(log n): The list is sorted and you keep dividing it in half like binary search does.
- O(1): Your friend is the first name lucky.
FAQs (Asymptotic Notation)
What does Big-O really mean?
Big-O shows how slow or fast an algorithm is when input grows. It is like a speed meter for your code.
Do I need to calculate Big-O for every code?
Not always. But it is good to know for common patterns like loops, nested loops, sorting, etc.
Why don’t we care about seconds and time taken?
Because time depends on computer, RAM, etc. But Big-O works on logic not on machine. So it is more universal.
What is the best Big-O?
O(1) is best that means it is constant. No matter if input is 10 or 10 million or time stays same.
Is Big-O always accurate?
It is a good estimate. Real world performance also depends on things like cache, compiler, etc but Big-O gives a good idea.
Can an algorithm have more than one notation?
Yes. For example, Quick Sort is-
- Best case: O(n log n)
- Worst case: O(n²)
- Average: O(n log n)
What if two algorithms have same Big-O?
Then you look at real performance, number of operations or constants involved.