Counting Sort Algorithm : Working, Advantages and Applications

In the world of computer science and data structures we have came across multiple sorting algorithms and techniques like Bubble Sort, Merge Sort, Quick Sort. These all algorithms are comparison based algorithms. If you want to cover the basics of algorithms like bubble sort, quick sort, merge sort, insertion sort and selection sort then we have already covered such algorithms in our series.

In today’s blog we will be covering one very special non-comparison based algorithm that is counting sort algorithm. We will explore how counting sort works, advantages, disadvantages and applications.

What is a Counting Sort Algorithm?

Counting Sort Algorithm is a non-comparison based algorithm like radix sort, bucket sort whereas bubble sort, merge sort, selection sort, insertion sort and quick sort all are comparison-based algorithm.

When we talk about counting sort then in this we have already range defined or either we can continue with the process by finding the maximum element from the given input array. Let’s look at an example where we have an array [3, 1, 3, 3, 2, 1, 2]

In this array we have maximum array is 3 and with the help of that we have to define the additional space to solve a particular sorting problem. To check the working of a counting sort algorithm we will have a look of different steps of doing that in the next section.

Working of Counting Sort Algorithm

In this section we are covering the working of counting sort algorithm step by step. Let’s begin by initialize array of input size [3, 1, 3, 3, 2, 1, 2].

Finding Maximum Element (Step 1)

To determine the size of the count array, we need to find the maximum element from the given input array. In our example 3 is the maximum element of the array.

So in this case we need a count array of size max + 1 i.e, 3 +1 = 4.

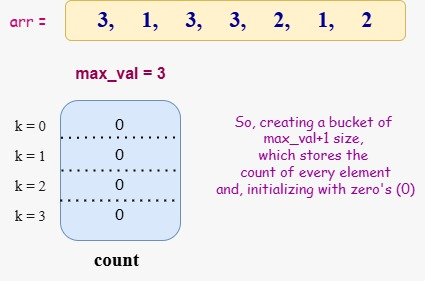
Initialize the Count Array

Now we have to create a count array of size 4 and initialize all the values by 0.

Count Array : [0, 0, 0, 0]

Count the Occurrences of Elements

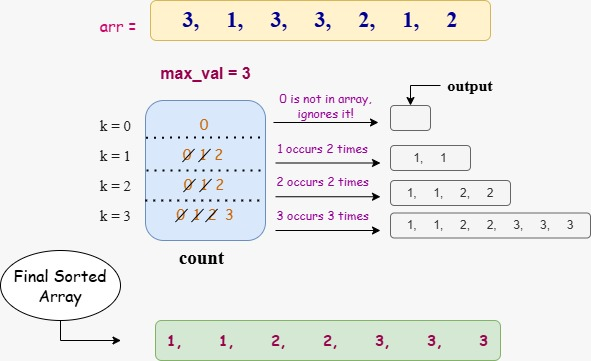
Go through the input array and count the number of occurrences of each value:

1. For 3: count[3] += 1 — count = [0, 0, 0, 1]
2. For 1: count[1] += 1 — count = [0, 1, 0, 1]
3. For 3: count[3] += 1 — count = [0, 1, 0, 2]
4. For 3: count[3] += 1 — count = [0, 1, 0, 3]
5. For 2: count[2] += 1 — count = [0, 1, 1, 3]
6. For 1: count[1] += 1 — count = [0, 2, 1, 3]
7. For 2: count[2] += 1 — count = [0, 2, 2, 3]

Final Count Array

Lastly we got our count and the final count array is [0, 2, 2, 3]

Build the Output Array

Create an output array of the same size as input: output = [0, 0, 0, 0, 0, 0, 0]

Now place each element from the input array into its sorted position using the count array (iterate in reverse for stability).

Final Array : [1, 1, 2, 2, 3, 3, 3]

Step	Description	Count Array	Output Array
Initial	Input array	[0, 0, 0, 0]	[_, _, _, _, _, _, _]
Count occurrences	Count of each number	[0, 2, 2, 3]	[_, _, _, _, _, _, _]
Cumulative count	Prefix sum of count array	[0, 2, 4, 7]	[_, _, _, _, _, _, _]
Place 2 (from index 6)	count[2] = 4 — place at index 3, count[2] -= 1	[0, 2, 3, 7]	[_, _, _, 2, _, _, _]
Place 1 (from index 5)	count[1] = 2 — place at index 1, count[1] -= 1	[0, 1, 3, 7]	[_, 1, _, 2, _, _, _]
Place 2 (from index 4)	count[2] = 3 — place at index 2, count[2] -= 1	[0, 1, 2, 7]	[_, 1, 2, 2, _, _, _]
Place 3 (from index 3)	count[3] = 7 — place at index 6, count[3] -= 1	[0, 1, 2, 6]	[_, 1, 2, 2, _, _, 3]
Place 3 (from index 2)	count[3] = 6 — place at index 5, count[3] -= 1	[0, 1, 2, 5]	[_, 1, 2, 2, _, 3, 3]
Place 1 (from index 1)	count[1] = 1 — place at index 0, count[1] -= 1	[0, 0, 2, 5]	[1, 1, 2, 2, _, 3, 3]
Place 3 (from index 0)	count[3] = 5 — place at index 4, count[3] -= 1	[0, 0, 2, 4]	[1, 1, 2, 2, 3, 3, 3]

Complexity Analysis of Counting Sort Algorithm

Complexity for the counting sort algorithm depends upon the input array and the additional space array that is counting array. I am initializing these terms with variable ‘n’ (input size) and ‘k’.

In the Best Case complexity analysis we got O(n+k), for average case complexity it is O(n+k) and for the worst case complexity it is O(n+k). The Space Complexity for the count sort algorithm is O(n+k) that depend upon the input size array and the count array.

Cases	Time Complexities
Best Case Time Complexity	O(n+k)
Average Case Time Complexity	O(n+k)
Worst Case Time Complexity	O(n+k)

Implementation of Counting Sort

In this section we are seeing the coding implementation of Counting Sort Algorithm in python programming language.

def counting_sort(arr):
    if not arr:
        return arr
    max_val = max(arr)
    min_val = min(arr)
    range_of_elements = max_val - min_val + 1
    count = [0] * range_of_elements
    output = [0] * len(arr)
    for num in arr:
        count[num - min_val] += 1
    for i in range(1, len(count)):
        count[i] += count[i - 1]
    for num in reversed(arr):
        output[count[num - min_val] - 1] = num
        count[num - min_val] -= 1
    return output

Output for the following code 

Advantages of Counting Sort

There are some advantages of counting sort algorithm over other sorting algorithms.

1. It has linear time complexity when the range of input is not much larger than the number of elements.
2. It is a stable sorting algorithm that keeps equal elements in their original order.
3. It does not use any comparison between elements during sorting.
4. It is easy to understand and implement with basic programming knowledge.
5. It works well for sorting large datasets with a small range of values.

Disadvantages of Counting Sort

There are some disadvantages of counting sort algorithm over other sorting algorithms.

1. It is not efficient when the range of input values is very large compared to the number of elements.
2. It uses extra space to store the count and output arrays, which increases memory usage.
3. It only works for non-negative integers or needs modifications for negative numbers.
4. It is not suitable for sorting data with floating-point numbers or strings directly.
5. It becomes less practical when dealing with very large numbers or a wide range of input values.

Applications of Counting Sort Algorithm

1. It is used in situations where the input data is limited to a small range of integers.
2. It is helpful in sorting characters or strings based on alphabetical order using ASCII values.
3. It is used in digital image processing where pixel values fall within a known range.
4. It can be applied in making histograms or frequency counts of elements quickly.
5. It is useful in scenarios that need stable and fast sorting for small-range numeric data.

FAQs (Counting Sort Algo)

What type of data is best suited for Counting Sort?

Counting Sort works best for sorting integers within a small, known range.

Is Counting Sort a comparison-based sorting algorithm?

No counting sort is not a comparison based algorithm.

Can Counting Sort handle negative numbers?

By default answer is no but it can be modified to handle negative numbers by shifting values.

Is Counting Sort a stable sorting algorithm?

Yes, Counting Sort maintains the relative order of equal elements.

What is the time complexity of Counting Sort?

Its time complexity is O(n + k), where n is the number of elements and k is the range of input values.