When you want to find the shortest way from one place to another, like the quickest road on Google Maps and in that you are using the logic behind Dijkstra’s Algorithm. This algorithm is used in computers to solve shortest path problems in graphs. A graph is just a group of points called nodes and connected by lines called edges. Dijkstra’s Algorithm helps figure out the minimum distance from a starting point to all other points in such a graph.
It is widely used in real life for GPS navigation, internet data routing, flight planning, and even video games. The best part is that it is not that hard to understand. If you are someone learning computer science, programming, or data structures then this is one of the most important algorithms to know. In this blog we will explain how Dijkstra’s Algorithm works, show its code, go over its complexity, and list its pros, cons, and real world uses.
What is Dijkstra’s Algorithm?
Dijkstra’s Algorithm is a famous method used to find the shortest path between two points in a graph. It is like finding the fastest way to reach your friend’s house on Google Maps. This algorithm was created by a computer scientist named Edsger Dijkstra. It works on graphs that have only positive weights which means it can not handle negative distances.
The main idea is to start from one point called the source and go step by step to find the shortest way to reach all other points. It is used in many real world tools like GPS systems, network routing, and games. Dijkstra’s Algorithm is fast and easy to understand which makes it a favorite for solving path problems.
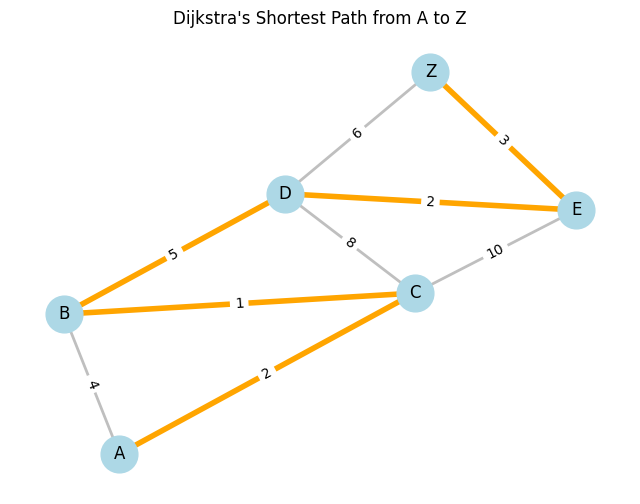
How Dijkstra’s Algorithm Works?
To understand how Dijkstra’s Algorithm works then think of it like finding the shortest way through a city map. You begin at one location and check all nearby paths to find the fastest one. Then you move to the next closest place and do the same.
Here is a step-by-step breakdown.
- Start from the source node. Set its distance to 0. All other nodes get infinity as their initial distance.
- Visit the node with the smallest known distance. In the beginning that is the source.
- Update the distances of its neighboring nodes. If the new path is shorter then replace the old value.
- Mark the current node as visited. Once visited then it would not be checked again.
- Repeat the steps until all nodes are visited or you have reached the destination.
This process ensures that you always find the shortest path in graphs with non-negative weights.
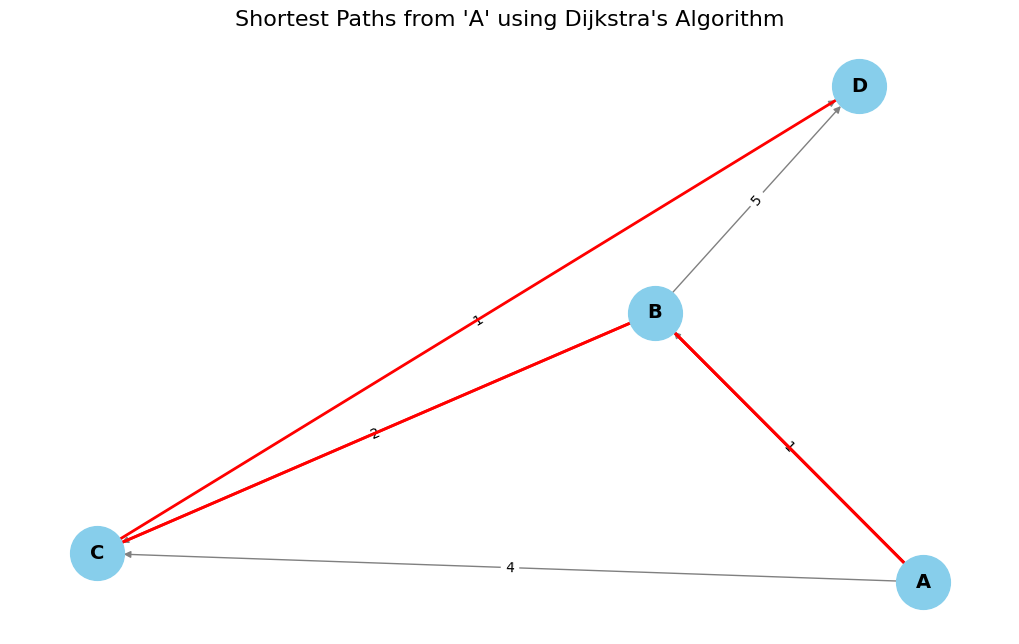
Python Implementation of Dijkstra’s Algorithm
pip install networkx matplotlib
import networkx as nx
import matplotlib.pyplot as plt
import heapq
def dijkstra(graph, start):
distances = {node: float('inf') for node in graph.nodes()}
distances[start] = 0
visited = set()
pq = [(0, start)]
paths = {node: [] for node in graph.nodes()}
paths[start] = [start]
while pq:
current_dist, current_node = heapq.heappop(pq)
if current_node in visited:
continue
visited.add(current_node)
for neighbor in graph.neighbors(current_node):
weight = graph[current_node][neighbor]['weight']
distance = current_dist + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
paths[neighbor] = paths[current_node] + [neighbor]
heapq.heappush(pq, (distance, neighbor))
return distances, paths
# Create graph
G = nx.DiGraph()
edges = [
('A', 'B', 1), ('A', 'C', 4),
('B', 'C', 2), ('B', 'D', 5),
('C', 'D', 1)
]
G.add_weighted_edges_from(edges)
# Run Dijkstra's Algorithm
start_node = 'A'
distances, paths = dijkstra(G, start_node)
# Draw the graph
pos = nx.spring_layout(G)
plt.figure(figsize=(10, 6))
# Draw all nodes and edges
nx.draw(G, pos, with_labels=True, node_color='skyblue', node_size=1500, font_size=14, font_weight='bold', edge_color='gray')
nx.draw_networkx_edge_labels(G, pos, edge_labels={(u, v): d['weight'] for u, v, d in G.edges(data=True)})
# Highlight shortest paths from source
for dest in G.nodes():
if dest != start_node and paths[dest]:
path_edges = list(zip(paths[dest], paths[dest][1:]))
nx.draw_networkx_edges(G, pos, edgelist=path_edges, edge_color='red', width=2)
plt.title(f"Shortest Paths from '{start_node}' using Dijkstra's Algorithm", fontsize=16)
plt.axis('off')
plt.show()
Time and Space Complexity of Dijkstra’s Algorithm
| Data Structure Used | Time Complexity | Space Complexity |
| Array (Naive Implementation) | O(V²) | O(V) |
| Binary Heap / Priority Queue | O((V + E) log V) | O(V + E) |
| Fibonacci Heap | O(E + V log V) | O(V + E) |
Advantages of Dijkstra’s Algorithm
- It helps find the shortest way from one place to all other places in a graph.
- You can use it on different types of graphs like one-way or two-way roads.
- It always gives the shortest path if the distances are not negative.
- The steps are simple so it is easy to write the code for it.
- Many apps like Google Maps and internet routers use this algorithm because it works well.
Disadvantages of Dijkstra’s Algorithm
- It does not work if some paths have negative distances.
- For very big graphs it can take a lot of time to finish.
- It needs all the graph data to be in memory so it uses a lot of space sometimes.
- It only finds shortest paths from one starting point at a time.
- For some special problems or other algorithms might work better and faster.
Applications of Dijkstra’s Algorithm
- It helps find the fastest way to reach your destination on maps like Google Maps or Apple Maps. This makes traveling easier and saves time.
- It helps send data through the internet by choosing the best path, so your messages and videos arrive quickly and safely.
- Airlines use it to plan flight routes that save fuel and time by picking the shortest or cheapest paths between airports.
- Video games use it so characters or players can find the shortest way through a game map or maze, making the game more fun and realistic.
- Robots use this algorithm to move around in factories or homes without bumping into objects and helping them do their jobs better.
Frequently Asked Questions
What is Dijkstra’s Algorithm?
Dijkstra’s Algorithm is a way to find the shortest path from one place to other places on a map or graph It helps you find the fastest or cheapest route to travel from one point to many others by checking all possible ways and choosing the best one.
Who invented Dijkstra’s Algorithm and when?
A smart computer scientist named Edsger W Dijkstra created this algorithm in 1956 He was from the Netherlands and his work helped computers solve path problems much faster and better than before.
Can Dijkstra’s Algorithm work with negative weights?
No this algorithm does not work if some paths have negative distances It only works when all the distances between points are zero or more If you have negative values you need to use a different method like Bellman Ford algorithm.
On which types of graphs can Dijkstra’s Algorithm be used?
You can use this algorithm on graphs where connections are one way or two way But the important thing is that all the distances or weights on those connections must be positive or zero If there are negative weights the results will not be correct.
How fast is Dijkstra’s Algorithm?
The speed depends on how you write the code If you use simple tools it can be slow for big graphs But when you use a priority queue it becomes much faster This helps the algorithm pick the next closest point quickly and avoid checking all points one by one.
What are the main uses of Dijkstra’s Algorithm?
This algorithm is used in many places It helps GPS apps find the fastest routes for traveling It helps send data on the internet by choosing the best path It helps airlines plan flight routes to save time and fuel It is also used in video games to find paths for characters and in robots to move around without bumping into things.
Does Dijkstra’s Algorithm find the shortest path to all points?
Yes this algorithm finds the shortest distance from the starting point to every other point in the graph This makes it very useful when you want to know the best ways to travel from one place to many different places at the same time.
Does Dijkstra’s Algorithm always find the best path?
Yes as long as the graph has no negative distances this algorithm will always find the shortest and best path It cannot handle negative weights so if there are any it might give wrong answers.
What data structures make Dijkstra’s Algorithm faster?
Using the right tools helps make the algorithm faster Priority queues or heaps are commonly used because they help pick the closest point to explore next very quickly This reduces the time the algorithm takes to find all shortest paths especially in big graphs.
Is Dijkstra’s Algorithm easy to learn and use?
Yes it is quite simple to understand and use The idea behind it is easy and many programming languages have built-in tools that make writing the algorithm easier Even beginners can learn and implement it with some practice.





![Top 10 Applications of Linked List Data Structure [2025]](https://www.iquanta.in/blog/wp-content/uploads/2025/02/WhatsApp-Image-2025-02-01-at-2.48.42-PM-218x150.jpeg)

