Dynamic Programming is very important concept when it comes to data structures and algorithms. It is one of the most powerful technique when it is a part of algorithm design and complex problem solving. Whether you are preparing for coding interviews, competitive programming, or working on complex software so understanding dynamic programming is really helpful for you.
In this blog we will talk about what is dynamic programming, when to use it, and how to master it with examples and real world applications.
What is Dynamic Programming?
Dynamic Programming is a method or approach in which we are breaking the larger problem into smaller sub-problem and a useful fundamental concept in computer science domain. Instead of solving same sub-problems multiple times, DP helps to solve each sub-problem only once and then stored the rest result in an array.
Dynamic Programming relies on two very important concepts and those are overlapping subproblems and optimal substructure. Overlapping subproblems are defined in such a manner that the same smaller problems appear again and again during computation.
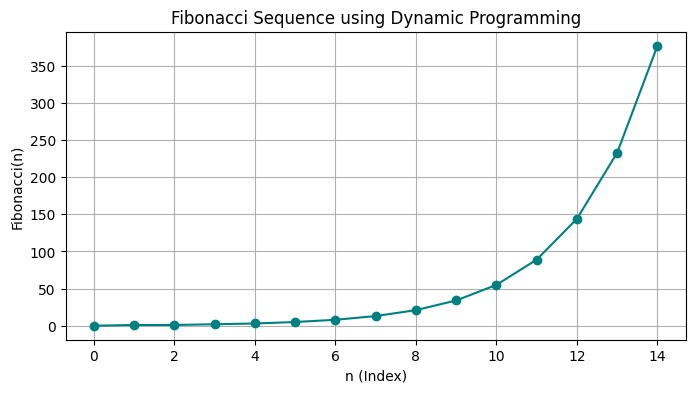
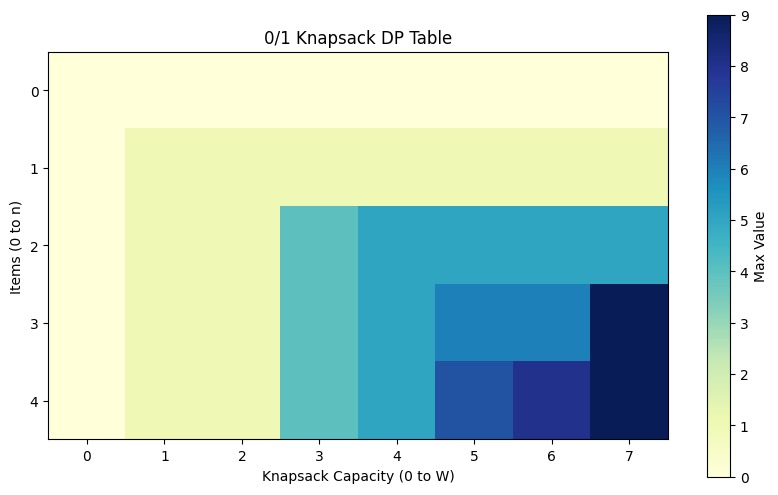
If I’m talking about the classic problems of dynamic programming that includes Fibonacci Sequence, 0/1 knapsack problems and LCS (Lowest Common Subsequence).
Key Characteristics of Dynamic Programming
There are few characteristics that we are dealing with dynamic programming includes :
- Optimal Substructures
- Overlapping Subproblems
- Top-Down Approach
- Bottom-Up Approach
- Reuse of Sub-problems
Dynamic Programming vs Divide and Conquer
In this section we will be talking about the difference between dynamic programming vs Divide and Conquer and explain their features in a tabular form.
| Feature / Criteria | Dynamic Programming (DP) | Divide and Conquer (D&C) |
| Problem Structure | Overlapping subproblems + optimal substructure | Independent subproblems + optimal substructure |
| Subproblem Repetition | Yes same subproblems are solved multiple times | No subproblems are solved once and are distinct |
| Approach | Bottom-Up (Tabulation) or Top-Down (Memoization) | Top-Down Recursive Approach |
| Storage/Memoization | Stores intermediate results to avoid recomputation | Does not store results – recomputes if needed |
| Optimization Goal | Focuses on computing optimal results (min/max/count) | Focuses on solving and combining results |
| Time Complexity | Generally lower due to reuse of subproblems (e.g., O(n)) | May be higher due to repeated calculations (e.g., O(n log n)) |
| Common Problems Solved | Fibonacci, Knapsack, LCS, Matrix Chain Multiplication | Merge Sort, Quick Sort, Binary Search, Strassen’s Matrix Multiplication |
| Programming Style | More iterative in Tabulation, sometimes recursive with Memoization | Purely recursive and often easier to implement initially |
| Space Complexity | May require extra space for DP tables or memo dictionaries | Often uses stack space due to recursion |
| Example | Fibonacci with memoization (O(n)) | Merge Sort (O(n log n)) |
| Goal of Reuse | Avoid solving the same problem multiple times | Divide and conquer independent problems |
| Best Suited For | Optimization and combinatorial problems | Sorting, searching, and numerical problems |
Types of Dynamic Programming
| DP Type | Definition | Use Case | Example Problem |
| 1. Memoization (Top-Down DP) | Solves problems by recursion + storing results of subproblems in a lookup table (usually a dictionary or array). | When recursion leads to overlapping subproblems and repeated calls. | Fibonacci Number (recursive with cache), 0/1 Knapsack (top-down) |
| 2. Tabulation (Bottom-Up DP) | Solves problems iteratively by filling up a DP table, usually from smaller subproblems to larger ones. | When the problem can be broken down into smaller subproblems and solved iteratively. | Coin Change, Longest Common Subsequence |
| 3. Space Optimized DP | Reduces space complexity by storing only necessary previous values instead of the full DP table. | When only a few recent values are needed to compute the current result. | Fibonacci (with two variables), LCS (1D space optimization) |
| 4. Bitmask DP | Uses bitmasking (binary representation of sets) to represent states efficiently. | Useful for subset-related or combinatorial problems. | Traveling Salesman Problem (TSP), Counting subsets |
| 5. Digit DP | Solves problems digit by digit using memoization, often used with numbers or ranges. | When constraints involve digits and number formations. | Count numbers with digits sum = K, Valid numbers in a range |
Popular Dynamic Programming Problems
- Fibonacci Numbers
- 0/1 Knapsack Problem
- Longest Common Subsequence
- Longest Increasing Subsequence
- Coin Change Problem
- Matrix Chain Multiplication
- Edit Distance
- Rod Cutting Problem
How to Identify a Dynamic Programming Problem
Competitive programmers are always thinking of the better way to solve the problem according to the best optimization approach and when it comes the dynamic programming there are several thing that we need to ask from ourselves that includes few questions.
- Can we divide the given problem into smaller sub-problems?
- Are those problems that we are dealing with are repeated?
- Is there any optimal way to combine those sub-solutions.
Step-By-Step Approach to Solve a DP Problems
There are some steps that is feasible to solve the problem in the dynamic programming and in this section we all are covering these steps simultaneously:
- First, you need to understand the problem and explain entire problem through brute force approach.
- Post this we need to identify the recursion relation.
- Optimize the memorization that is your top-down approach.
- Convert to the tabulation for if needed.
- Reduce the space complexity (it is an optional part as not that necessary tasks to be performed).
Applications of Dynamic Programming
Sure! Here are the 5 applications of Dynamic Programming in simple, one-line, human-written style:
- Google Maps uses DP to find the shortest and fastest routes between locations.
- Vending machines use it to calculate the minimum number of coins needed for change.
- Auto-correct systems apply DP to fix spelling errors using edit distance.
- Bioinformatics tools use DP to compare DNA sequences and find genetic similarities.
- Project planners rely on DP to allocate resources efficiently under constraints.
Top-Down vs Bottom-Up Code Examples
def fibonacci(n, memo={}):
# Base cases
if n <= 1:
return n
# Check if already solved
if n in memo:
return memo[n]
# Solve and store in memo
memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
return memo[n]
# Example usage
print(fibonacci(10)) # Output: 55
Frequently Asked Questions
What is the main idea behind Dynamic Programming?
The main idea behind Dynamic Programming is to avoid solving the same problem repeatedly. Instead of recalculating answers for the same subproblems, it stores the results once and reuses them when needed. This saves a lot of time and makes programs more efficient. It’s especially useful when the problem has overlapping subproblems and an optimal substructure.
What are real-life examples of Dynamic Programming?
Dynamic Programming is used in many real-life scenarios such as optimizing delivery routes (like Google Maps), predicting text or spelling corrections (using Edit Distance), analyzing DNA sequences in biology, and even planning investments. These are problems where making the best decision at each step depends on results from previous steps.
Is DP hard to learn for beginners?
It may seem hard at first, especially because it involves breaking problems into subproblems and thinking recursively or iteratively. But once you understand the pattern identify subproblems, use memoization or tabulation, and reuse solutions so that it becomes much easier. With practice and consistent problem-solving, anyone can master it.