Graph coloring is like playing with crayons but instead of coloring pictures you are coloring dots called nodes in a graph. The rule is simple. If two dots are connected with a line they cannot have the same color. That is it. You are just trying to color each dot in such a way that no two connected ones clash.
This idea might sound silly at first but it is actually very useful. Think about making an exam timetable. You do not want two subjects with the same group of students to happen at the same time. Graph coloring helps fix that. It is also used in map coloring so countries do not share colors. It is used in solving puzzles like Sudoku and even in mobile networks.
In this blog we will break it down step by step. What graph coloring means how to do it using a greedy algorithm its pros and cons real life uses and a simple Python code to try it yourself.
What is Graph coloring?
Imagine you are trying to color a bunch of dots that are connected by lines. The rule is simple. Dots that are connected should not have the same color. That is what graph coloring is all about.
In computer science terms, these dots are called vertices or nodes and the lines are called edges. When we color each vertex in such a way that no two connected vertices have the same color, we say the graph is properly colored.
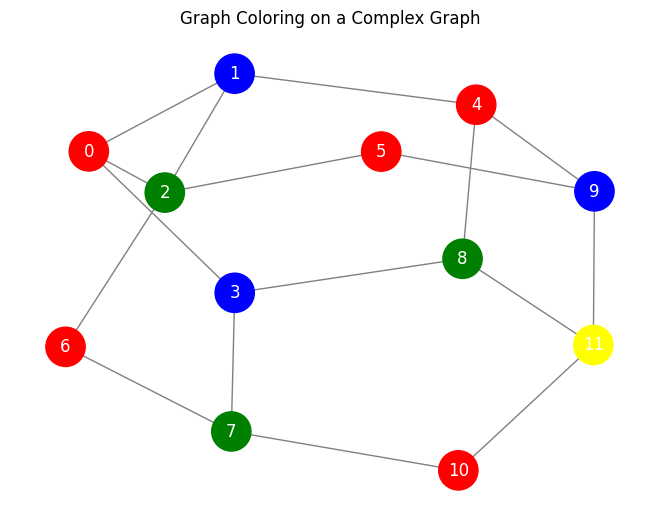
The goal is to use as few colors as possible while still following the rule. The smallest number of colors needed to color a graph this way is called the chromatic number. Here is a fun example. If you have three friends and each one hates sitting next to the others in class, how many benches or colors do you need to keep them apart. Graph coloring helps solve problems like that.
What is Greedy Algorithm?
A greedy algorithm is a method that makes the best choice at every single step, without thinking too far ahead. It is kind of like grabbing the first good option you see and hoping it works out well in the end.
In graph coloring, a greedy algorithm works like this. You pick one node and give it the first color. Then you move to the next node and give it the smallest color that is not already used by its neighbors. You keep doing this until all nodes are colored.
It does not always give the perfect answer, but it is fast and easy. For example, if there are better ways to color with fewer colors, greedy might miss it. But most of the time, it does a pretty good job, especially when you just need something quick and simple. So, greedy means quick decisions, not always perfect, but often good enough.
How Graph Coloring Algorithm Works?
Let us now see how the graph coloring algorithm actually works step by step. We will use the greedy approach to keep things simple and fast.
- Start with the first node in the graph.
- Give it the first color. For example, Color 0.
- Move to the next node.
- Look at its neighbors. Check which colors are already used by them.
- Pick the smallest color number that is not used by any of its neighbors.
- Repeat the same process for every node in the graph.
By the end, every node will have a color, and no two connected nodes will share the same color.
Python Implementation of Graph Coloring Algorithm
def greedy_graph_coloring(graph):
n = len(graph)
result = [-1] * n
result[0] = 0
for u in range(1, n):
used_colors = [False] * n
for v in graph[u]:
if result[v] != -1:
used_colors[result[v]] = True
for color in range(n):
if not used_colors[color]:
result[u] = color
break
return result
graph = {
0: [1, 2],
1: [0, 2, 3],
2: [0, 1],
3: [1]
}
colors = greedy_graph_coloring(graph)
print("Color assigned to each node:", colors)
Advantages of Graph Coloring
- Simple and fast to implement using greedy algorithm.
- Helps in creating conflict-free schedules and timetables.
- Optimizes resource allocation like rooms or frequencies.
- Useful in solving puzzles and logic-based problems.
- Widely applicable in real-world tasks like map coloring and compiler design.
Disadvantages of Graph Coloring
- Greedy algorithm does not always find the optimal solution and may use more colors than actually needed.
- Finding the minimum number of colors required (chromatic number) is very hard for large and complex graphs.
- Graph coloring problems are NP-complete which means they become extremely difficult to solve as the graph size grows.
- Performance may drop if the input graph has many nodes and edges, especially without good heuristics.
- Not suitable for dynamic graphs where nodes or edges change frequently, as the algorithm may need to rerun from scratch.
Applications of Graph Coloring
- Timetable Scheduling: Assigns time slots to classes or exams so that no student has two exams at the same time.
- Map Coloring: Ensures that no two neighboring countries or states share the same color, making maps easier to read.
- Register Allocation in Compilers: Assigns variables to limited CPU registers without overlapping during execution.
- Mobile and Wi-Fi Networks: Assigns frequencies or channels to towers or routers so signals don’t interfere.
- Puzzle Solving: Uses coloring concepts to ensure rules are followed without repetition in rows or columns.
FAQs
What is graph coloring in simple words?
Graph coloring is a way of assigning different colors to the parts of a graph so that no two connected nodes have the same color. It helps in organizing things without conflict, like in maps, schedules or network systems.
What is the main goal of graph coloring?
The main aim is to color all nodes in a graph using the fewest number of colors possible. This should be done while making sure that no two connected nodes share the same color.
Is graph coloring only used in computer science?
No it is widely used in real-life areas like exam timetables, map designs, mobile towers and Wi-Fi channels. Besides computer science industries like education, telecom and logistics also benefit from it.
What type of algorithm is used in graph coloring?
The greedy algorithm is commonly used which assigns colors step-by-step in a fast and efficient way. Though simple it may not always find the most optimal coloring with the fewest colors.
Can we always get the perfect coloring with greedy method?
Not necessarily as the greedy method depends on the order of nodes and might use extra colors. It is quick and easy but may not find the best solution in every case.