Sorting is a common task in programming, and the insertion sort algorithm is one of the easiest ways to understand how sorting works. If you are just starting with algorithms or preparing for interviews then this guide is all you need to understand the insertion sort algorithm from the ground up.
What is Insertion Sort Algorithm?
The insertion sort algorithm is a simple and beginner-friendly method used to sort elements in a list. It works just like how we sort playing cards in our hands. Imagine you are holding a few unsorted cards. You pick one card at a time and place it in the correct position among the cards you’ve already sorted. You keep doing this until all the cards are in order.
In the same way, the insertion sort algorithm starts from the second element in a list which compares it with the elements before it and inserts it into its right position. This process continues until the whole list is sorted.
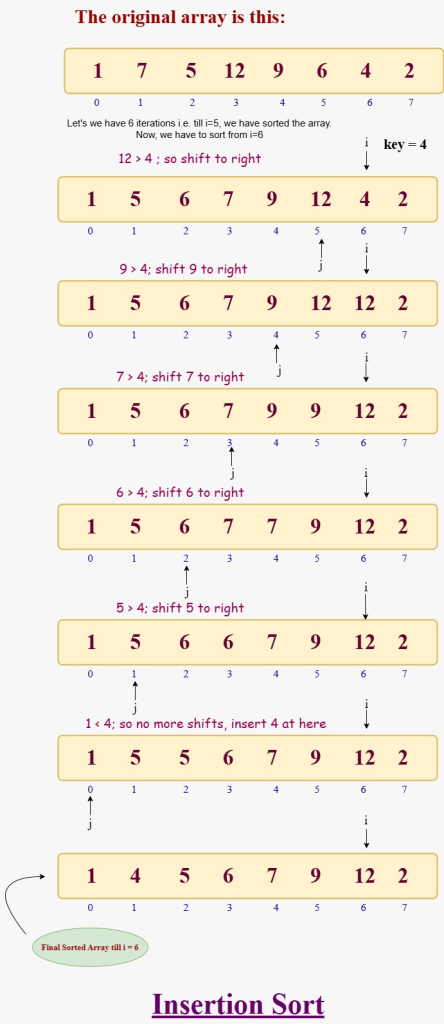
Let’s walk through a step-by-step example using this list:
[1, 7, 5, 12, 9, 6, 4, 2]
We assume the first element 1 is already sorted. Now we go through each element one by one:
- Compare 7 with 1 – Since 7 is greater, it stays where it is.
Array = [1, 7, 5, 12, 9, 6, 4, 2] - Compare 5 with 7 – 5 is smaller, so we move 7 to the right and insert 5 before it.
Array = [1, 5, 7, 12, 9, 6, 4, 2] - Compare 12 with 7 – 12 is greater, no change needed.
Array = [1, 5, 7, 12, 9, 6, 4, 2] - Compare 9 with 12 – 9 is smaller, move 12 and insert 9 before it.
Array = [1, 5, 7, 9, 12, 6, 4, 2] - Compare 6 with 12, 9, and 7 – Move all three to the right and insert 6 at the correct place.
Array = [1, 5, 6, 7, 9, 12, 4, 2] - Compare 4 with 12, 9, 7, 6, and 5 – Move all these and place 4 after 1.
Array = [1, 4, 5, 6, 7, 9, 12, 2] - Compare 2 with 12 down to 1 – Shift all greater elements and place 2 after 1.
Resultant Array = [1, 2, 4, 5, 6, 7, 9, 12]
How Insertion Sort Work?
The insertion sort algorithm starts from the second element of the list and assumes the first one is already sorted. Then it compares each new element with the sorted portion and inserts it in the right place.
Step-by-Step Explanation
Let’s consider an example list:
[5, 3, 4, 1, 2]
- In Phase 1 Current element = 3
- Compare with 5 and shift 5 to the right
- Insert 3 at index 0
- List becomes: [3, 5, 4, 1, 2]
Phase 2
- Current element = 4
- Compare with 5 and shift 5
- Compare with 3 and no shift
- Insert 4 after 3
- List becomes: [3, 4, 5, 1, 2]
Phase 3
- Current element = 1
- Shift 5, 4, 3
- Insert 1 at index 0
- List becomes: [1, 3, 4, 5, 2]
4th Step
- Current element = 2
- Shift 5, 4, 3
- Insert 2 after 1
- Final sorted list: [1, 2, 3, 4, 5]
Complexity Analysis of Insertion Sort
| Step | Current Element | Comparison Elements | Action Taken |
|---|---|---|---|
| 1 | 7 | [1] | 7 > 1 Keep 7 in place |
| 2 | 5 | [1, 7] | 5 < 7 Move 7 and Insert 5 before it |
| 3 | 12 | [1, 5, 7] | 12 > 7 Keep in place |
| 4 | 9 | [1, 5, 7, 12] | 9 < 12 Move 12, Insert before it |
| 5 | 6 | [1, 5, 7, 9, 12] | 6 < 9 Shift 9, 7 → Insert after 5 |
| 6 | 4 | [1, 5, 6, 7, 9, 12] | 4 < 5 Shift multiple, insert after 1 |
| 7 | 2 | [1, 4, 5, 6, 7, 9, 12] | 2 < 4 Shift multiple, insert after 1 |
In the second table which is mentioned below we are comparing Insertion Sort with Other Algorithm like Bubble Sort, Selection Sort, Merge Sort and Quick Sort.
| Sorting Algorithm | Time (Best) | Time (Avg) | Time (Worst) | Space | Stable | Use Case |
|---|---|---|---|---|---|---|
| Insertion Sort | O(n) | O(n²) | O(n²) | O(1) | Yes | Small or nearly sorted arrays |
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) | Yes | Educational use and very simple |
| Selection Sort | O(n²) | O(n²) | O(n²) | O(1) | No | When swaps are more expensive than comparisons |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes | Large datasets |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) | No | Fastest in practice |
Implementation of Insertion Sort in C++
#include <iostream>
using namespace std;
// Function to perform insertion sort
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
// Shift elements greater than key to the right
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
// Function to print the array
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver code
int main() {
int arr[] = {1, 7, 5, 12, 9, 6, 4, 2};
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original array:\n";
printArray(arr, n);
insertionSort(arr, n);
cout << "Sorted array:\n";
printArray(arr, n);
return 0;
}
Implementation of Insertion Sort in Python
def insertion_sort(arr):
# Traverse from 1 to len(arr)
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
# Move elements of arr[0..i-1], that are greater than key, one position ahead
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
# Driver code
arr = [1, 7, 5, 12, 9, 6, 4, 2]
print("Original array:")
print(arr)
insertion_sort(arr)
print("Sorted array:")
print(arr)
Advantages of Insertion Sort Algorithm
- Simple to implement and understand.
- Efficient for small or nearly sorted datasets.
- In-place sorting with stable behavior.
Disadvantages of Insertion Sort Algorithm
- Insertion Sort is slow for large datasets because its time complexity is O(n²).
- It is not ideal for large or completely unsorted data as it performs poorly in such cases.
- It requires a lot of comparisons and shifting of elements in the worst case which makes it inefficient.
FAQs (Insertion Sort Algorithm)
What is the insertion sort algorithm used for?
The insertion sort algorithm is mainly used to sort small datasets or nearly sorted arrays. It’s a great choice when performance is not the top priority but simplicity and clarity are.
Is insertion sort better than bubble sort?
Yes, insertion sort usually performs better than bubble sort. It does fewer comparisons and swaps in practice, especially when the data is already partially sorted.
Does insertion sort work in-place?
Yes, insertion sort is an in-place sorting algorithm. It doesn’t require any extra memory space and modifies the original array directly during the sorting process.