Kadane’s Algorithm is one of the most amazing technique which is used to solve maximum sub-array problems. It involves finding the continuous sub-arrays with a one dimensional array of numbers that has the largest sum. So, whether you are preparing for coding interviews or try to analyze multiple data analysis problems or queries, then Kadane’s algorithm is really great and comes in picture.
This concept is used to solve the possible subarray that take O(n^2) time complexity to cover algorithm. It scans the array only once and also used to update maximum sum along with. Because of this simplicity and high performance of algorithm makes it most widely used among developers and enthusiasts.
In this blog we will be talking about Kadane’s Algorithm, working and implementation, analyze it’s time complexity, and real-life applications. Whether you are a fresher or brushing up with your DSA concepts, this guide really helpful for you to understand this concept.
What is Kadane’s Algorithm?
Kadane’s Algorithm is an important concept among developers where you are using dynamic programming techniques to find the maximum sum of subarray. The main idea behind this algorithm is to scan the particular array from left to right.
This compares the array at every steps and try to find the maximum value so far. By tracking the maximum value found so far, Kadane’s Algorithm efficiently solves the problem in linear time (O(n)), making it highly useful for performance-critical tasks like financial data analysis or coding competitions.
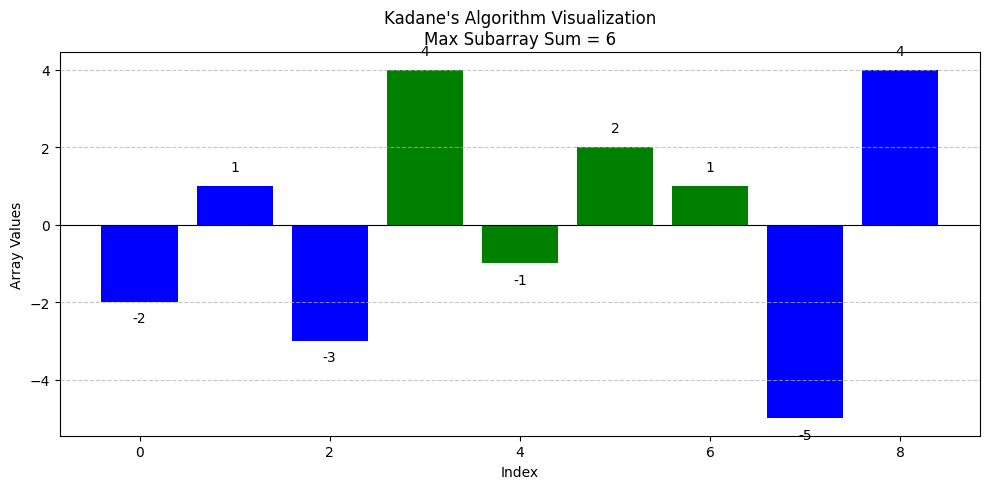
Kadane’s Algorithm Working (Step-By-Step)
Kadane’s algorithm works by scanning the array from left to right. It uses two variables –
- max_current: Maximum sum ending at current position.
- max_global: The highest value max_current has ever reached.
| Step | Index | arr[i] | max_current = max(arr[i], max_current + arr[i]) | max_global = max(max_global, max_current) | Start Index | End Index |
| 1 | 0 | -2 | -2 | -2 | 0 | 0 |
| 2 | 1 | 1 | max(1, -2 + 1) = 1 | max(-2, 1) = 1 | 1 | 1 |
| 3 | 2 | -3 | max(-3, 1 – 3) = -2 | max(1, -2) = 1 | ||
| 4 | 3 | 4 | max(4, -2 + 4) = 4 | max(1, 4) = 4 | 3 | 3 |
| 5 | 4 | -1 | max(-1, 4 – 1) = 3 | max(4, 3) = 4 | 4 | |
| 6 | 5 | 2 | max(2, 3 + 2) = 5 | max(4, 5) = 5 | 5 | |
| 7 | 6 | 1 | max(1, 5 + 1) = 6 | max(5, 6) = 6 | 6 | |
| 8 | 7 | -5 | max(-5, 6 – 5) = 1 | max(6, 1) = 6 | ||
| 9 | 8 | 4 | max(4, 1 + 4) = 5 | max(6, 5) = 6 |
Understand the Problem
Kadane’s Algorithm helps find the maximum sum of numbers that are next to each other in a list. It checks whether to continue adding or start fresh at each step.
def max_subarray_brute_force(arr):
max_sum = float('-inf')
start_idx = end_idx = 0
for i in range(len(arr)):
current_sum = 0
for j in range(i, len(arr)):
current_sum += arr[j]
if current_sum > max_sum:
max_sum = current_sum
start_idx = i
end_idx = j
print(f"Brute Force -> Max Sum: {max_sum}, Subarray: {arr[start_idx:end_idx+1]}")
return max_sum
def kadane_algorithm(arr):
max_current = max_global = arr[0]
start = end = s = 0
for i in range(1, len(arr)):
if arr[i] > max_current + arr[i]:
max_current = arr[i]
s = i
else:
max_current += arr[i]
if max_current > max_global:
max_global = max_current
start = s
end = i
print(f"Kadane's Algorithm -> Max Sum: {max_global}, Subarray: {arr[start:end+1]}")
return max_global
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
print("Original Array:", arr)
print("-" * 50)
max_subarray_brute_force(arr)
kadane_algorithm(arr)
Kadane’s Algorithm Code
When I’m talking about Kadane’s algorithm then there are different approaches to solve and run the particular problem and approach. We will start here with the Brute Force Approach in C++, Java & Python programming language.
Kadane’s Brute Force Approach in C++
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int maxSubarrayBruteForce(vector<int>& arr) {
int maxSum = INT_MIN;
int start = 0, end = 0;
for (int i = 0; i < arr.size(); i++) {
int currentSum = 0;
for (int j = i; j < arr.size(); j++) {
currentSum += arr[j];
if (currentSum > maxSum) {
maxSum = currentSum;
start = i;
end = j;
}
}
}
cout << "Max Sum: " << maxSum << ", Subarray: ";
for (int k = start; k <= end; k++) cout << arr[k] << " ";
cout << endl;
return maxSum;
}
int main() {
vector<int> arr = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
maxSubarrayBruteForce(arr);
return 0;
}
Kadane’s Brute Force Approach in Java
public class MaxSubarrayBruteForce {
public static int maxSubarray(int[] arr) {
int maxSum = Integer.MIN_VALUE;
int start = 0, end = 0;
for (int i = 0; i < arr.length; i++) {
int currentSum = 0;
for (int j = i; j < arr.length; j++) {
currentSum += arr[j];
if (currentSum > maxSum) {
maxSum = currentSum;
start = i;
end = j;
}
}
}
System.out.print("Max Sum: " + maxSum + ", Subarray: ");
for (int k = start; k <= end; k++) {
System.out.print(arr[k] + " ");
}
System.out.println();
return maxSum;
}
public static void main(String[] args) {
int[] arr = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
maxSubarray(arr);
}
}
Kadane’s Brute Force Approach in Python
def max_subarray_brute_force(arr):
max_sum = float('-inf')
start_idx = end_idx = 0
for i in range(len(arr)):
current_sum = 0
for j in range(i, len(arr)):
current_sum += arr[j]
if current_sum > max_sum:
max_sum = current_sum
start_idx = i
end_idx = j
print(f"Max Sum: {max_sum}, Subarray: {arr[start_idx:end_idx+1]}")
return max_sum
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
max_subarray_brute_force(arr)
Time Complexity Analysis of Kadane’s Algorithm
In this section we will be talking about the time complexity of Kadane’s algorithm in data structures in almost every possible case.
| Feature / Metric | Brute Force Approach | Kadane’s Algorithm |
| Time Complexity | O(n²) | O(n) |
| Space Complexity | O(1) | O(1) |
| Nested Loops Used? | Yes (Two loops to check every subarray) | No (Single pass through array) |
| Performance on Small Arrays | Acceptable | Excellent |
| Performance on Large Arrays | Slow and inefficient | Very fast and optimized |
| Best Case Time Complexity | O(n²) | O(n) |
| Worst Case Time Complexity | O(n²) | O(n) |
| Average Case Time Complexity | O(n²) | O(n) |
| Real-Time Use Case Friendly? | No | Yes |
| Interview Use | Rarely used, only to explain concept | Commonly asked and expected |
| Code Simplicity | Simple but inefficient | Simple and efficient |
| Use of Extra Space | None | None |
FAQs (Frequently Asked Questions)
What is Kadane’s Algorithm used for?
Kadane’s Algorithm is used to find the maximum sum of a contiguous subarray within a one-dimensional array. It solves the Maximum Subarray Problem efficiently in linear time, making it ideal for real-time data analysis and competitive programming.
What is the time complexity of Kadane’s Algorithm?
The time complexity of Kadane’s Algorithm is O(n), where n is the number of elements in the array. Unlike the brute-force approach, Kadane’s Algorithm only makes a single pass through the array, making it much faster and more efficient.
Can Kadane’s Algorithm handle arrays with all negative numbers?
Yes Kadane’s algorithm handle arrays with all negative numbers