In computer science, Kruskal’s Algorithm is a way to find the minimum connections between points or nodes in a graph without making a loop. It is mostly used when we want to connect all parts of a network using the least possible total weight or cost. For example, connecting cities with roads or setting up computer networks. It is named after Joseph Kruskal, who introduced this algorithm in 1956. The main idea is to keep adding the shortest available edge to the final solution as long as it does not form a cycle.
It works well on graphs with fewer edges, also known as sparse graphs. It is one of the most common algorithms to find minimum spanning trees in a weighted graph.
In this blog, we will learn how Kruskal’s Algorithm works, its pros and cons, compare it with Prim’s Algorithm, and also look at its real-life uses and Python code.
What is Kruskal’s Algorithm?
Kruskal’s Algorithm is a well-known method used to find the Minimum Spanning Tree in a connected, undirected, and weighted graph. A Minimum Spanning Tree is a set of edges that connects all the nodes in the graph without any cycles and with the minimum possible total weight.
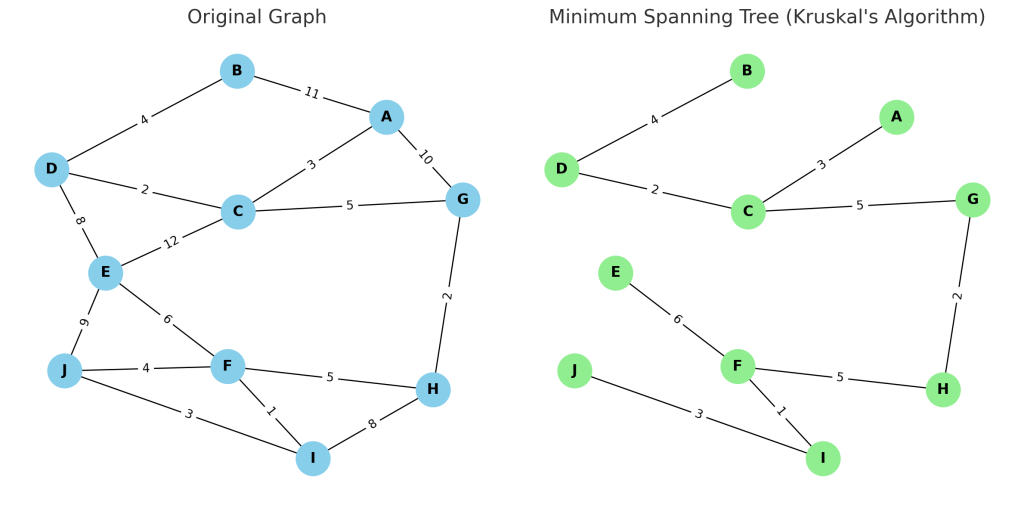
The algorithm follows a greedy approach. It works by first sorting all the edges in order of their weights from smallest to largest. Then it starts picking the shortest edge that doesn’t form a cycle with the edges already chosen. This process continues until all the nodes are connected.
Kruskal’s Algorithm is especially useful in practical scenarios like designing computer networks, laying telephone lines, building roads between cities or anything that requires connecting multiple points with the lowest cost. In short Kruskal’s Algorithm helps in finding the cheapest way to connect all parts of a system without creating loops.
How Kruskal’s Algorithm Works?
Kruskal’s Algorithm finds the Minimum Spanning Tree of a graph. It first sorts all edges by their weight, from smallest to largest. Then it picks the smallest edge and adds it to the MST if it does not create a cycle. To check for cycles the algorithm uses a Union-Find data structure. It repeats this process, adding the next smallest edge that keeps the graph connected without cycles. The algorithm stops when all vertices connect in the MST.
Kruskal’s Algorithm vs Prim’s Algorithm
| Feature | Kruskal’s Algorithm | Prim’s Algorithm |
| Approach | Greedy, edge-based | Greedy, vertex-based |
| Suitable for | Sparse graphs | Dense graphs |
| Edge Selection | Picks smallest edge globally | Picks smallest edge from MST vertices |
| Data Structure Used | Union-Find (Disjoint Set) | Priority Queue (Min-Heap) |
| Cycle Detection | Yes via Union-Find | Not required explicitly |
| Time Complexity | O(E log E) | O(E log V) |
| MST Construction | Adds edges one by one | Grows MST by adding vertices |
| Graph Type | Works on disconnected graphs | Requires connected graphs |
| Initialization | Starts with edges, no initial vertex | Starts from an arbitrary vertex |
| Memory Usage | Less memory for sparse graphs | More memory for dense graphs |
| Implementation | Simpler to implement | Slightly more complex |
| Edge Sorting Required | Yes | No |
| Performance in Practice | Faster for sparse graphs | Faster for dense graphs |
Advantages of Kruskal’s Algorithm
- Works well for sparse graphs with fewer edges.
- Simple and easy to implement using sorting and Union-Find.
- Finds the Minimum Spanning Tree efficiently.
- Can handle disconnected graphs and finds a Minimum Spanning Forest.
- Always chooses the smallest available edge, ensuring optimal MST.
- Uses less memory compared to some other MST algorithms on sparse graphs.
Disadvantages of Kruskal’s Algorithm
- Sorting all edges can be slow for very large graphs.
- Not efficient for dense graphs with many edges.
- Requires a good Union-Find implementation to avoid high time complexity.
- Can be harder to implement correctly compared to some other MST algorithms.
- May not perform well when the graph is already connected and dense.
Time and Space Complexity of Kruskal’s Algorithm
| Algorithm | Time Complexity | Space Complexity |
| Kruskal’s Algorithm | O(E log E) | O(E + V) |
| Prim’s Algorithm | O(E log V) | O(V) |
| Dijkstra’s Algorithm | O(E + V log V) | O(V) |
Python Implementation of Kruskal’s Algorithm
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x, y):
rootX = self.find(x)
rootY = self.find(y)
if rootX == rootY:
return False
if self.rank[rootX] < self.rank[rootY]:
self.parent[rootX] = rootY
elif self.rank[rootX] > self.rank[rootY]:
self.parent[rootY] = rootX
else:
self.parent[rootY] = rootX
self.rank[rootX] += 1
return True
def kruskal(n, edges):
edges.sort(key=lambda x: x[2])
uf = UnionFind(n)
mst = []
for u, v, w in edges:
if uf.union(u, v):
mst.append((u, v, w))
return mst
# Example usage
n = 4
edges = [
(0, 1, 10),
(0, 2, 6),
(0, 3, 5),
(1, 3, 15),
(2, 3, 4)
]
mst = kruskal(n, edges)
print("Edges in the Minimum Spanning Tree:")
for u, v, w in mst:
print(f"{u} - {v} : {w}")
FAQs (Kruskal’s Algorithm)
What type of graph does Kruskal’s Algorithm work on?
Kruskal’s Algorithm works on both connected and disconnected weighted graphs. For disconnected graphs, it finds a Minimum Spanning Forest.
How does Kruskal’s Algorithm avoid cycles?
It uses a Union-Find (Disjoint Set) data structure to check if adding an edge will create a cycle. If the vertices of the edge belong to the same set, adding it would form a cycle, so the edge is skipped.
When should I use Kruskal’s Algorithm over Prim’s Algorithm?
Use Kruskal’s Algorithm when the graph is sparse with fewer edges. Prim’s Algorithm performs better on dense graphs with many edges.
What is the time complexity of Kruskal’s Algorithm?
The time complexity is O(E log E), mainly due to sorting the edges, where E is the number of edges.
Can Kruskal’s Algorithm be used for directed graphs?
No, Kruskal’s Algorithm is designed for undirected graphs to find a Minimum Spanning Tree.
Conclusion
Kruskal’s Algorithm is a popular and efficient method to find the Minimum Spanning Tree of a graph, especially when the graph is sparse. It works by sorting edges and adding the smallest edges one by one while avoiding cycles.
Using the Union-Find data structure helps keep the process fast and effective. Though it may not be the best choice for very dense graphs, its simplicity and performance make it a valuable algorithm to know. Understanding Kruskal’s Algorithm is important for solving many real-world problems involving network design, clustering, and more.