Bubble Sort Algorithm with Complexity Analysis

We have completed all the basic data structures which includes Arrays, Linked List, Queues. Stacks, Graphs and Trees. To look after the complexity behind the work with these structures we need different algorithms.

As algorithm is the step by step process to complete a particular task, which includes the complexity analysis that is time and space complexities. In this blog we will be covering bubble sort algorithm, covering its implementation in C and C++ programming languages, complexity analysis along with its advantages and disadvantages.

What is Bubble Sort Algorithm?

Bubble Sort Algorithm is a simple algorithm to sort the array by comparing the adjacent elements. It is a sorting algorithm that repeatedly continue the steps of swapping the larger value with the small one.

Let’s understand with the basic example of Bubble Sort Algorithm in which we are introducing an unsorted array of 5 elements [ 1, 7, 3, 15, 2]. In this example we have taken these 5 elements which is stored in array in an unsorted manner and need to sort this array with the bubble sort algorithm.

Step 1: First we need to check the first two pair of adjacent elements 1 and 7. In this the larger element is at the end so no need to change anything. Instead of that need to check next two distinct elements.

Resultant array after 1st step : [1, 7, 3, 15, 2].

Step 2 : Need to check next adjacent elements which are 7 and 3. Now in this case larger element is at start, we need to take it at the end.

Resultant array after step 2 : [1,3, 7, 15, 2]

Step 3: Now need to compare other two adjacent element and in that case larger element is 15 and hence no need to change.

Resultant array after step 3 : [1, 3, 7, 15, 2]

Step 4: It is the final check of first cycle of bubble sort algorithm to sort an array. In this we need to check next two elements 15 and 2 . Now in this again we need to take 15 to the end.

Resultant array after 4th step : [1, 3, 7, 2, 15]

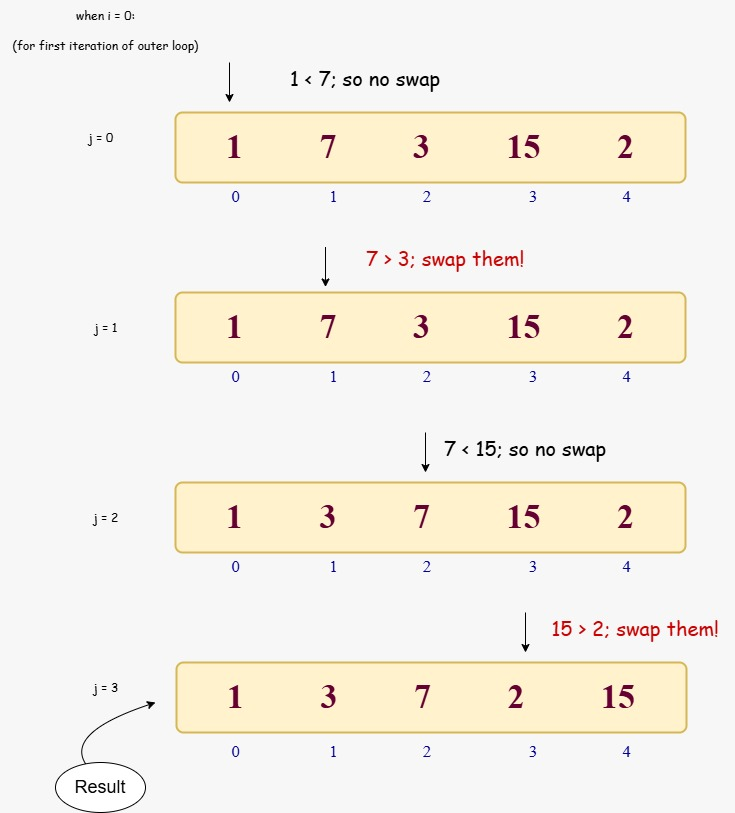
Hence we have completed our first cycle here and we will continue similar steps until and unless we are not getting our array in a sorted manner. I will not prefer to use this algorithm with complex and large datasets as it’s having high complexity.

How Bubble Sort Works?

The bubble sort algorithm is a simple sorting technique that repeatedly compares adjacent elements in a list and swaps them if they are in the wrong order. This process is repeated until the list is sorted.

Imagine the elements in an array as bubbles. The largest bubble (element) “bubbles up” to the end of the array with each full pass through the list. This continues until no more swaps are needed, which means the array is sorted.

Step-by-Step Working of Bubble Sort Algorithm

1. Start at the beginning of the array.
2. Compare the first two elements.
3. Swap them if the first is greater than the second (for ascending order).
4. Move to the next pair of adjacent elements and repeat the comparison and swap if necessary.
5. Continue this process until the end of the array — this completes one pass.
6. Repeat the entire process for the remaining unsorted part of the array.
7. Stop when a complete pass is made without any swaps — the array is now sorted.

Example:

Let’s sort the array: [5, 2, 9, 1]

1. First pass: [5, 2, 9, 1] → [2, 5, 9, 1] → [2, 5, 9, 1] → [2, 5, 1, 9]
2. Second pass:[2, 5, 1, 9] → [2, 5, 1, 9] → [2, 1, 5, 9]
3. Third pass:[2, 1, 5, 9] → [1, 2, 5, 9]
4. Fourth pass: No swaps needed. Sorting is complete.

The final sorted array is [1, 2, 5, 9].

Implementation of Bubble Sort Algorithm in C

#include <stdio.h>

// Function to perform Bubble Sort
void bubbleSort(int arr[], int n) {
    int temp;
    int swapped;

    for (int i = 0; i < n - 1; i++) {
        swapped = 0;  // Flag to optimize and break early if no swaps

        for (int j = 0; j < n - i - 1; j++) {
            // Compare adjacent elements
            if (arr[j] > arr[j + 1]) {
                // Swap if elements are in wrong order
                temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = 1;
            }
        }

        // If no two elements were swapped, the array is already sorted
        if (swapped == 0)
            break;
    }
}

// Function to print the array
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// Main function
int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("Original array:\n");
    printArray(arr, n);

    bubbleSort(arr, n);

    printf("Sorted array:\n");
    printArray(arr, n);

    return 0;
}

Implementation of Bubble Sort Algorithm in C++

#include <iostream>
using namespace std;

// Function to perform Bubble Sort
void bubbleSort(int arr[], int n) {
    bool swapped;

    for (int i = 0; i < n - 1; i++) {
        swapped = false;

        // Loop through the array up to the unsorted part
        for (int j = 0; j < n - i - 1; j++) {
            // Swap if the elements are in the wrong order
            if (arr[j] > arr[j + 1]) {
                swap(arr[j], arr[j + 1]);
                swapped = true;
            }
        }

        // If no elements were swapped, the array is already sorted
        if (!swapped)
            break;
    }
}

// Function to print the array
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << endl;
}

// Main function
int main() {
    int arr[] = {64, 25, 12, 22, 11};
    int n = sizeof(arr) / sizeof(arr[0]);

    cout << "Original array:" << endl;
    printArray(arr, n);

    bubbleSort(arr, n);

    cout << "Sorted array:" << endl;
    printArray(arr, n);

    return 0;
}

Complexity Analysis of Bubble Sort Algorithm

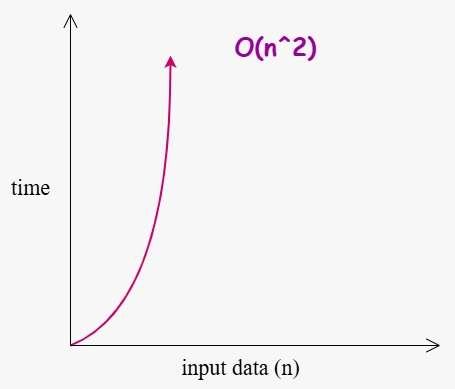
Complexity Analysis of bubble sort algorithm is O(n^2). Here is a detailed below about the complexity analysis of bubble sort algorithm.

Case	Time Complexity	Explanation
Best Case	O(n)	When the array is already sorted (only one pass needed with no swaps).
Average Case	O(n²)	On average, each element is compared with every other element.
Worst Case	O(n²)	When the array is sorted in reverse order (maximum number of swaps).
Space Complexity	O(1)	In-place sorting no additional memory required.
Stability	Yes	Bubble Sort is stable and it does not change the relative order of equal elements.
Adaptive	Yes	If optimized with a swap flag, it can adapt and exit early if sorted.

Advantages and Disadvantages of Bubble Sort

If I am specifically taking about bubble sort then we will see there are some advantages are there to use this algorithm but at the same point due to complexity there are several disadvantages too.

Advantages of Bubble Sort

1. Bubble Sort does not require additional memory space.
2. Easy to understand and implement.
3. It is useful for teaching basic sorting concepts and algorithm design.

Disadvantages of Bubble Sort

1. It performs too many unnecessary comparisons and swaps, making it inefficient for large input sizes.
2. Due to its time complexity, it is much slower than advanced algorithms like merge sort.
3. It is not widely used in many real world applications due to its poor performance.