Tree data structure is an important data structure to maintain hierarchical computation in the system. To maintain complex data systems we are using tree data structure by following different terms that involves nodes, height, depth as well as generation of a tree in data structures.
In this blog we will talk about tree traversal algorithms along with recapping the old ones. Tree traversal algorithms include pre order traversal, post order traversal, inorder traversal and level order traversal. Tree traversal algorithms help in efficient searching or traversing a node in a tree and along with that we can update or change the data during traversal in a tree. Comparison between pre order and post order traversal is an important task to be performed.
What is a Tree Data Structure?
Tree data structure is a versatile data structure that stores data in a hierarchical form. In a tree there are different nodes that are connected through the edges and each node contains data and pointers helps to connect different nodes with each other.
Root Node
Root Node in the tree serves as a topmost node. It is the initial point in the tree to reach all other nodes. All the nodes of the tree data structure are directly or indirectly connected to it and the flow of entire tree decides from the root node itself.
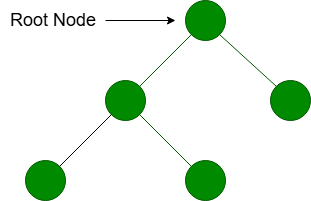
Node
It is a basic terminology which represents data in a tree that are connected with each other through the edges. Node in a tree contains data that we need to store and apart from that A, B, C, D, root all are the nodes given below in the diagram 1.1
Edge
Edge is a connection between two nodes in a tree that joins two nodes together. It’ s main property is to show the relationship between the child node and parent node. It is very important term in a tree to understand relationship between the nodes.
Parent node in tree
A parent node in tree is a node which has one or more child nodes. Example: In the diagram Node A is the parent node of Node B and Node C.
Leaf Node : Leaf nodes in a tree have no child nodes. Example : Node B, Node C, Node D serve as a leaf node in the given diagram.
Height : Height of a tree can be calculated as the longest path from that node to the leaf node.
Height of a tree = Height of a root node.
Depth of a tree : Depth of a tree can be calculated as the number of edges between the root node to the respective node.
Level of a tree : Level of a tree in a data structure can be calculated as the number of connections formed between the root node and the respective node.
Example : Root Node == Level 0 (root node of a tree is at level 0)
Generations : All the nodes of the same level are considered to be the same generation nodes.
Example : Node A ,Node D == Level 1
Node B, Node C== Level 2
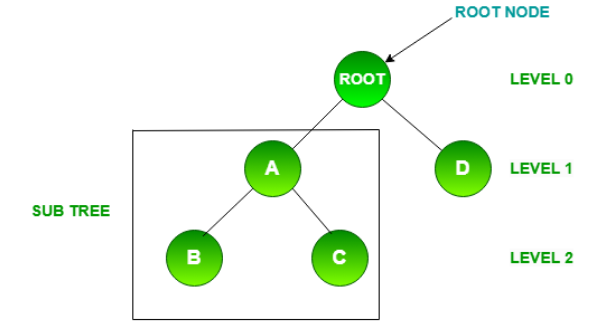
Degree of a node : Degree of a tree can be calculated as the total number of children count of that node.
Degree of a node = Total number of children of a node
What is Tree Traversal?
Tree traversal is the process of visiting every node in a tree structure in a specific order. A tree is a type of data structure that looks like a family tree or a chart, where each node can have children. But how do we visit all the nodes without missing anyone or repeating them. That’s where tree traversal algorithms come in.
They guide us on how to move through the tree, one node at a time. There are four main types which includes pre order traversal, post order traversal, inorder traversal, and level order traversal. Each method follows a different path and is useful for different tasks, like printing, copying, or deleting a tree. Choosing the right traversal helps solve problems easily.
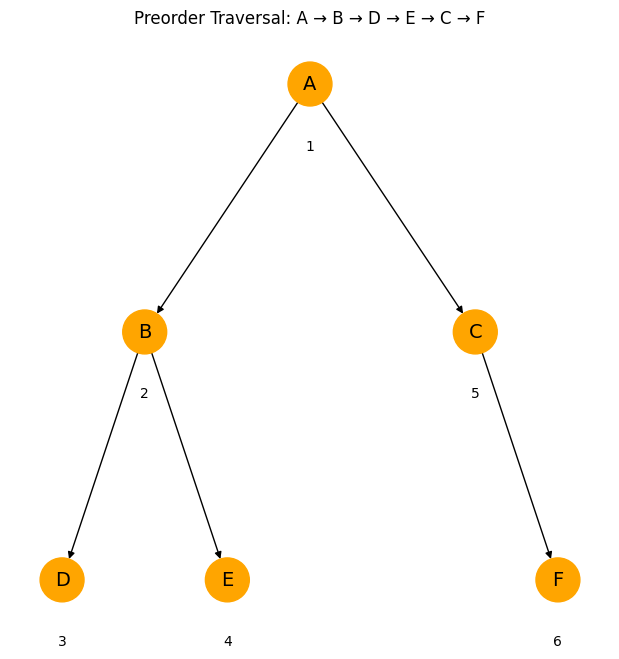
Pre Order Traversal Algorithm
In pre order traversal, we follow a specific order that is visiting the root node first, then move to the left child, and finally go to the right child. So the pattern is: Root → Left → Right.
Imagine you are meeting your own family. You talk to the parent first, then the left child, and then the right child. This approach helps when you want to copy a tree because it starts with the main part first. In coding it is useful when you need to deal with parent nodes before working on the children. This traversal works well in many situations where early access to the root node is important. Even though it is simple where pre order traversal plays a big role in many tree-based algorithms.
Post Order Traversal Algorithm
Post order traversal follows a different pattern where first you are visiting the left child, then the right child, and last the root node. So the order becomes finally Left → Right → Root.
Think of it like solving the smaller problems before dealing with the bigger one. This method is useful when you need to delete a tree. You remove the children first and then remove the parent which keeps things clean and avoids errors. It is also used in some mathematical expression trees where you calculate the values at the bottom first. Even though post order traversal seems like you are saving the main part for the end that helps a lot when the final result depends on all smaller parts being handled first.
Inorder Traversal Algorithm
Inorder traversal goes in this sequence like the way we are representing here Left → Root → Right. You should first visiting the left child, then the root node, and then the right child. This type of traversal is very important when working with Binary Search Trees. Because it gives you the nodes in sorted order.
So if your tree holds numbers or words, an inorder traversal will show them in order from smallest to largest. This makes it perfect for printing sorted data or checking the structure of the tree. It is also helpful when you want to look at data in a balanced way. Even though it sounds basic, inorder traversal is often the most-used technique in many tree-based operations.
Time Complexity of Tree Traversal Algorithms
Understanding the time complexity of tree traversal algorithms is important for analyzing the efficiency of operation on a tree data structure. No matter which tree traversal method we are using whether it is pre order traversal, Inorder traversal, post order traversal, or level order traversal in which every node in the tree is usually visited one time. This means the time it takes depends mostly on how many nodes the tree has. In this section, we will look at how long each method takes so you can understand how fast they work in different situations.
| Traversal Type | Time Complexity | Explanation |
| Pre-order Traversal | O(n) | Each node is visited once (Root → Left → Right) |
| In-order Traversal | O(n) | Each node is visited once (Left → Root → Right) |
| Post-order Traversal | O(n) | Each node is visited once (Left → Right → Root) |
| Level-order Traversal (BFS) | O(n) | Each node is visited once using a queue (Breadth-First Search) |
Comparison Between Pre Order and Post Order Traversal
In this section we will talk about the comparison between pre order traversal and post order traversal algorithm. We will understand multiple features in the tabular format.
| Aspect | Pre-order Traversal | Post-order Traversal |
| Order of Traversal | Root → Left Subtree → Right Subtree | Left Subtree → Right Subtree → Root |
| Visit Time of Root Node | First | Last |
| Use Case | Used to create a copy of the tree | Used to delete or free nodes in a tree |
| Expression Evaluation | Used to get prefix expression from an expression tree | Used to get postfix expression from an expression tree |
| Recursive Algorithm Pattern | Process root, then recursively traverse left and right | Recursively traverse left and right, then process root |
| Example (for tree 1-2-3) | Pre-order: 1 → 2 → 3 | Post-order: 2 → 3 → 1 |
| Stack Implementation Order | Push right, then left (so left is processed first) | Push root last (after left and right children) |
| Memory Usage | Similar, but can vary based on recursion depth | Similar, but can vary based on recursion depth |
Frequently Asked Questions
What are tree traversal algorithms?
Tree traversal algorithms help you visit each node in a tree structure exactly once. These methods include pre order traversal, post order traversal, inorder traversal, and level order traversal. Since each follows a specific visiting pattern, they solve different problems like expression evaluation, data searching, or hierarchical processing.
Why do tree traversal algorithms matter in computer science?
These algorithms play a key role in solving problems that involve hierarchical or tree-like data. Developers use them in various fields such as compilers, databases, and artificial intelligence. Tree traversal algorithms help simplify tasks like searching, analyzing, and modifying tree-based data structures.
What is the difference between pre order traversal and post order traversal?
In pre order traversal, you visit the root node first, then the left subtree, and finally the right subtree. On the other hand, post order traversal visits the left subtree first, then the right one, and the root comes last. This order matters depending on whether you need to process a parent node before or after its children.
When should you use inorder traversal?
Use inorder traversal when you want nodes in sorted order, especially in binary search trees. It visits nodes in the order of left, root, and right, which gives a sorted result. This makes it a great choice for tasks like sorting or printing tree elements in increasing order.
How does level order traversal stand out?
Unlike the other depth-first traversal methods, level order traversal follows a breadth-first approach. It uses a queue to visit all nodes level by level, from top to bottom and left to right. Because of this pattern, it’s ideal for printing each level or finding the shortest path in an unweighted tree.
Which traversal method works best for copying a tree?
Pre order traversal is the most useful when you need to copy a tree. Since it starts from the root and visits each node in order, it helps maintain the parent-child structure in the new tree.
Can you perform tree traversal without recursion?
Yes, you can use iterative methods with stacks or queues instead of recursion. In fact, all common tree traversal algorithms—like inorder, pre order, and post order that can be written without recursive calls. This approach is helpful when you want more control over memory usage.
Do all tree traversal algorithms have the same time complexity?
Yes, they do. Every node gets visited once, so the time complexity for inorder traversal, pre order traversal, post order traversal, and level order traversal is O(n), where n is the total number of nodes.
Where do we use tree traversal algorithms in real life?
You can find tree traversal algorithms in many real-world applications. For example, compilers use them for syntax tree analysis, databases for query plans, AI for decision trees, and file systems for folder navigation. Each method offers a different way to read or modify tree data based on the task.
Can we use these algorithms for N-ary trees?
Yes, you can apply them to N-ary trees as well. Although these trees have more than two children per node, the main idea of traversal remains the same. You only need to adjust your loop or recursive function to handle more children.

![Top 10 Applications of Linked List Data Structure [2025]](https://www.iquanta.in/blog/wp-content/uploads/2025/02/WhatsApp-Image-2025-02-01-at-2.48.42-PM-218x150.jpeg)

