Previously we have already covered graph data structure and the working with graph or trees, finding the shortest path in a way is the challenging process. That’s where BFS or Breadth First Search comes in a picture.
Whether your are going for competitive programming challenges or revising concept of graphs BFS (graph traversal algorithm) is an important concept to learn. If we will look at the real world examples, then we are using BFS everywhere which includes your tracking or navigating through a map, solving puzzles in AI, as well as crawling webpages and many more.
In this blog or tutorial we are coving what is BFS, why we are using it, covering intuition with visual diagrams, working of breadth first search algorithm, pseudocode, implementation in Java and Python along with the applications of BFS in real world.
What is BFS?
Breadth First Search or BFS is a graph traversal algorithm in which we are traversing to nodes in a level order (level by level). BFS is using queue data structure for performing traversal operation.
If you were standing at the center of a maze and could only walk to directly connected paths first then explore those paths then later you had be following the BFS strategy.
Let’s see an example for a better understanding of BFS algorithm in graph.
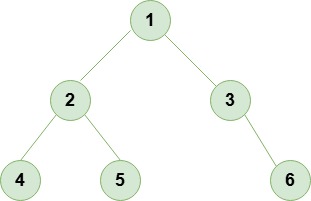
In this we are taking a graph and we want to track each node through BFS. Let’s represent this graph in an adjacency list format :
graph = {
1: [2, 3],
2: [4, 5],
3: [6],
4: [],
5: [],
6: []
}
We use a queue to track nodes and a set to keep visited ones.
| Step | Queue | Visited Nodes |
| 1 | [1] | {} |
| 2 | [2, 3] | {1} |
| 3 | [3, 4, 5] | {1, 2} |
| 4 | [4, 5, 6] | {1, 2, 3} |
| 5 | [5, 6] | {1, 2, 3, 4} |
| 6 | [6] | {1,2,3,4,5} |
| 7 | [] | {1,2,3,4,5,6} |
Why Use Breadth First Search?
If anyone is thinking why BFS is important then answer lies in the efficiency of algorithm. It is a graph traversal algorithm that explore the nodes layer by layer. This means if you are solving problems where every step or edge has the same cost such as mazes, grid-based pathfinding, or social networking, BFS is the perfect algorithm to find the shortest route.
One of the most common application of BFS is tree traversal particularly in the level order scenario where each node traversed level by level. In the real world, Breadth First Search is used in web crawlers to explore hyperlinks, in peer-to-peer networks like BitTorrent to search and distribute files and in GPS systems used to find optimal paths. Social media platforms like Facebook and LinkedIn also use BFS to find shortest connection paths between users, such as mutual friends or degrees of separation.
BFS Algorithm Intuition (with Visual Diagram)
Lets start with the basic example of BFS algorithm, assume a city where each building is connected through roads. So the logic behind that now you need to visit neighbours layer by layer. And this is the same intuition behind the BFS or Breadth First Search.
It is a powerful algorithm that uses queue data structure to keep a track record of visiting node where you need to traverse each node by level by level rather directly going in the depth.
BFS(Graph, start_node):
Create a queue Q
Mark start_node as visited
Enqueue start_node into Q
While Q is not empty:
current_node = Q.dequeue()
Process current_node (e.g., print it)
For each neighbor of current_node:
If neighbor is not visited:
Mark neighbor as visited
Enqueue neighbor into Q
Step-by-Step Working of BFS
In this section we are talking about the step by step process of how BFS or Breadth First Search algorithm works. Let’s have a look on the diagram given below to understand the working of BFS.
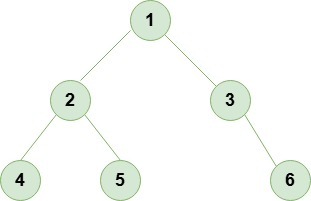
Start at the root node 1: We add it to the queue and mark it as visited.
Step 1: It is the first in the queue. We visit it then print or store the value and then enqueue its left child 2 and right child 3.
Step 2: We visit 2 then enqueue its left child 4 and right child 5.
Step 3: We visit 3 and since it has only a right child, we enqueue 6.
Step 4: We visit 4 as it has no children so nothing is added to the queue.
Step 5: We visit 5 and since it also has no children we move on.
Step 6: We visit 6 as the last node in the queue. It has no children.
BFS Pseudocode
This pseudocode shows a standard Breadth First Search (BFS) traversal on a graph or tree. It begins by creating an empty queue to explore nodes in a First-In, First-Out (FIFO) manner.
The starting node is marked as visited to prevent revisiting and is added to the queue. The algorithm then enters a loop that continues until the queue is empty which indicating that all reachable nodes have been visited.
BFS(Graph, start_node):
Create an empty queue Q
Mark start_node as visited
Enqueue start_node into Q
While Q is not empty:
current_node = Q.dequeue()
Process current_node (e.g., print it)
For each neighbor of current_node:
If neighbor is not visited:
Mark neighbor as visited
Enqueue neighbor into Q
BFS in Python & Java (with explanation)
The first code represents the implementation of BFS in Python Programming Language.
from collections import deque
def bfs(graph, start):
visited = set()
queue = deque([start])
result = []
while queue:
node = queue.popleft()
if node not in visited:
visited.add(node)
result.append(node)
queue.extend(graph[node])
return result
# Example graph (adjacency list representation)
graph = {
1: [2, 3],
2: [4, 5],
3: [6],
4: [],
5: [],
6: []
}
print(bfs(graph, 1))
Next is the same implementation but now this time it is Java Programming Language.
import java.util.*;
public class BFS {
public static List<Integer> bfsTraversal(Map<Integer, List<Integer>> graph, int start) {
Set<Integer> visited = new HashSet<>();
Queue<Integer> queue = new LinkedList<>();
List<Integer> result = new ArrayList<>();
queue.add(start);
while (!queue.isEmpty()) {
int node = queue.poll();
if (!visited.contains(node)) {
visited.add(node);
result.add(node);
queue.addAll(graph.getOrDefault(node, new ArrayList<>()));
}
}
return result;
}
public static void main(String[] args) {
Map<Integer, List<Integer>> graph = new HashMap<>();
graph.put(1, Arrays.asList(2, 3));
graph.put(2, Arrays.asList(4, 5));
graph.put(3, Arrays.asList(6));
graph.put(4, new ArrayList<>());
graph.put(5, new ArrayList<>());
graph.put(6, new ArrayList<>());
System.out.println(bfsTraversal(graph, 1));
}
}
Applications of BFS in Real World
There are various applications of Breadth First Search in real life and that are very useful which includes –
- Finding the shortest path in unweighted maps and road networks.
- Crawling web pages level by level in search engines.
- Solving puzzles like Rubik Cube using minimum moves.
- Network broadcasting to reach all connected devices.
- Detecting levels of friends in social networking sites.
Time and Space Complexity
If I’m talking about the time complexity of BFS algorithm is O(V+E) where V is the number of vertices and E is the number of edges. O(V+E) represents the visiting of each and every node level by level.
| Aspect | Complexity |
| Time Complexity | O(V+E) |
| Space Complexity | O(V) |
BFS vs DFS
| Feature | BFS (Breadth First Search) | DFS (Depth First Search) |
| Traversal Type | Level-wise (layer by layer) | Depth-wise it goes deep before backtracking |
| Data Structure | Queue | can be recursive call stack |
| Use Case | Shortest path in unweighted graphs | Detecting cycles, topological sort |
| Time Complexity | O(V+E) | O(V+E) |
| Space Complexity | queue + visited | stack + visited |
| Order of Node Visit | Visits neighbors first | Visits child nodes deeply first |
| Memory Usage | Usually more memory due to queue | Usually less memory than BFS |
BFS Interview Questions
Here are few interview question that are really helpful for you to implement this concept.
- Implement BFS traversal of a graph.
- Implement DFS traversal of a graph (both recursive and iterative).
- Find the shortest path in an unweighted graph using BFS.
- Detect a cycle in an undirected graph using DFS.
- Detect a cycle in a directed graph using DFS.
- Check if a graph is connected using BFS or DFS.
- Check whether a graph is bipartite using BFS.
- Count the number of islands in a 2D grid using DFS.
- Clone a graph using BFS or DFS.
- Perform topological sort using DFS.
Know More About BFS
What is the main purpose of BFS in graph traversal?
BFS is primarily used to explore nodes level by level. It is especially useful for finding the shortest path in unweighted graphs and for searching or spreading processes like in social networks or we
How is BFS different from DFS?
BFS uses a queue and explores neighbors before going deeper while DFS uses a stack or recursion and dives deep into one branch before backtracking. BFS ensures the shortest path in unweighted graphs, unlike DFS.
What are the real world applications of BFS?
BFS is used in shortest path algorithms, web crawling, network broadcasting, friend suggestions in social media and solving puzzles.
Conclusion
Breadth-First Search (BFS) is a powerful and fundamental algorithm in computer science especially useful for traversing or searching tree and graph data structures. Its ability to find the shortest path in unweighted graphs makes it ideal for real world applications. Understanding BFS not only strengthens your knowledge of algorithms but also equips you for tackle many graph based problems in interviews and practical development.



![Top 10 Applications of Linked List Data Structure [2025]](https://www.iquanta.in/blog/wp-content/uploads/2025/02/WhatsApp-Image-2025-02-01-at-2.48.42-PM-218x150.jpeg)

