CAT 2019 Quant Question Paper with Solution (Slot 1)

CAT 2019 Quant Solution

Q.1) Let x and y be positive real numbers such that
log₅ (x + y) + log₅ (x − y) = 3, and log₂ y − log₂ x = 1 − log₂ 3. Then xy equals

a)250

b)100

c)150

d)25

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]c)150[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Given

log₅ (x + y) + log₅ (x − y) = 3  and

log₂ y − log₂ x = 1 − log₂ 3.

log₅ (x + y) + log₅ (x − y) = log₅ (x^2-y^2) = 3

=>x^2-y^2=5^3…..eq1

log₂ y − log₂ x = 1 − log₂ 3

log₂ (y/x) = log₂ 2 − log₂ 3

log₂ (y/x) = log₂ 2/3

y/x=2/3

x=3y/2…..putting this in eq1

9y^2/4-y^2=125

5y^2/4=125

y^2=100

y=10

x=15

xy=150

[/bg_collapse]

Q.2) In a class, 60% of the students are girls and the rest are boys. There are 30 more girls than boys. If 68% of the students, including 30 boys, pass an examination, the percentage of the girls who do not pass is

a)20%

b)30%

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)20%[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

G girls

B boys

Let G=60x

B=40x

40x+30=60x

X=1.5

So, G=90

B=60

Total passed=150*68/100=102

Among 102 passed students, 30 are passed boys

So girls passed=102-30=72

So girls failed=total girls-girls passed=90-72=18

So % of girls failed=(18/90)*100=20%

[/bg_collapse]

Q.3) A person invested a total amount of Rs 15 lakh. A part of it was invested in a fixed deposit earning 6% annual interest, and the remaining amount was invested in two other deposits in the ratio 2 : 1, earning annual interest at the rates of 4% and 3%, respectively. If the total annual interest income is Rs 76000 then the amount (in Rs lakh) invested in the fixed deposit was

a)9 lakh

b)8 lakh

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)9 lakh[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Total =15 lakh

Let the amount invested in fixed deposit be = x at 6% SI

Remaining amount= 15-x ….which was invested in 2:1 at rates 4% and 3% per annum.

So amount invested at 4% pa=2/3(15-x)

Amount invested at 3% pa=1/3(15-x)

Total interest after 1 year=76000

So, (x*6*1)/100 + [2/3(15-x)*4*1]/100 + [1/3(15-x)*3*1]/100 = 76000

X=9 lakh

So 9 lakh will be the answer. 

[/bg_collapse]

Q.4) Three men and eight machines can finish a job in half the time taken by three machines and eight men to finish the same job. If two machines can finish the job in 13 days, then how many men can finish the job in 13 days?

a)13

b)23

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)13 lakh[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

X denotes men

M denotes machines.

Work be W

(3X+8M)*t/2=W

(8X+3M)*t=W

Dividing both equations

(3X+8M)/(8X+3M)=2

3X+8M=16X+6M

13X=2M

Also given

2M*13=W

So, W=26M

Let K men finish Work W in 13 days

So, W/(K*X)=13…

26M/(K*2M/13)=13

K=13 [/bg_collapse]

Q.5) The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala’s income goes down by 4% and Bimala’s goes up by 10%, then the percentage by which Kamala’s income would exceed Bimala’s is nearest to

a)31%

b)24%

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)31%[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

A=1.2B

A=0.8K

If K now becomes 0.96K and B now becomes 1.1B

Since B and K have a relation with A so, let us equate them

1.2B=0.8K

K=1.5B

So (New K -New B)/New B= ?

(0.96K-1.1B)/1.1B=[(1.44B-1.1B)/1.1B] * 100 = 0.34B/1.1B * 100=30.9 %

Which is close to 31% [/bg_collapse]

Q.6) Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is

a)2/3

b)2/4

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)2/3[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution: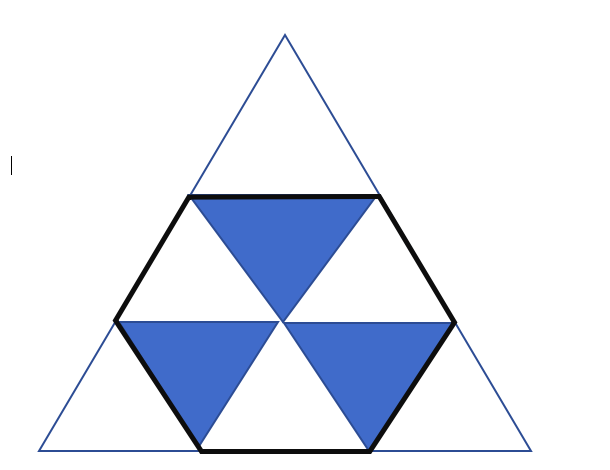

 

We can see that the equilateral triangle is made up of 9 equal triangles

Hexagon is made up of 6 equal triangles of same size

So ratio of areas = 6/9=2/3

[/bg_collapse]

Q.7) At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency?

a)8

b)6

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)8[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Let W be the work and a,b be the efficiencies of a and b

12(a+b)=W…..eq1

If A works at a/2 and b work at 3b per day.

Then 9(a/2+3b)=W…..eq2

Equating  equations 1 and 2

12a+12b=9a/2+27b

15a/2=15b

a=2b

so we need W/a

putting a=2b in eq1

W/a=8

[/bg_collapse]

Q.8) 

a)

b)

c)

d)

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

 

Solution: 

[/bg_collapse]

Q.9) Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is

a)53

b)51

c)48

d)49

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)51[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

22 students in total

R=82.5

Let sum of marks of all 22 students = 22A

Where A is the average marks of all 22 students

Given  The average score of the 21 students other than Gautam is 62  So

(22A-G)/21=62..eq1

Then

The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh

So, A= (22A-82.5)/21 +1

Solving this equation A=61.5

Putting this in eq1

G=51

[/bg_collapse]

Q.10) 

a)1/3

b)1

c)3

d)2/3

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)1/3[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

5.55^x=1000

5.55=1000^1/x ….eq1

0.555^y=1000

0.555=1000^1/y…..eq2

Dividing eq 1 and 2

1/10=1000^(1/x-1/y)

So 1/x – 1/y=1/3

[/bg_collapse]

Q.11)

a)-12

b)-20

c)-16

d)-24

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)-12[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

2^(19/2 +4+3n)*3^(4+2m)=2^(3/2+4m)*3^(n)

Comparing powers of 2 and 3 in LHS and RHS

3n+12=4m

4m-3n=12

And

4+2m=n

2m-n=-4

Solving both

n=-20

m=-12

[/bg_collapse]

Q.12) The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157:3, then the sum of the two numbers is

a)80

b)50

c)58

d)95

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)50[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

xy=616

also

(x^3-y^3)/(x-y)^3=157/3

Now x^3-y^3=(x-y)(x^2+y^2+xy)

So

(x^2+y^2+xy)/(x^2+y^2-2xy)=157/3

Let x^2+y^2=t

So

(t+616)/(t-1232)=157/3

t=1268

x^2+y^2=1268

(x+y)^2-2xy=1268

(x+y)^2-2*616=1268

(x+y)^2=2500

x+y=50

[/bg_collapse]

Q.13) Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is

a)70

b)75

c)80

d)60

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)70[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Let total marks be x

Meena scored 0.4x

After review marks are increased by 50%

So new marks=0.4x*1.5=0.6x

But she still fails by 35 marks

So passing mark=0.6x+35

Now if this post review score is increased by 20%

So it becomes 1.2*0.6x ,she gets 7 marks more than passing marks

That means passing marks =1.2*0.6x-7=0.72x-7

Equating passing marks in both the cases

0.6x+35=0.72x-7

0.12x=42

X=350

So passing marks=350*0.6+35=245

So percentage marks required to pass=245/350 *100=70%

[/bg_collapse]

Q.14) In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is

a)3.5

b)0.5

c)1.5

d)2.5

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)0.5[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

 

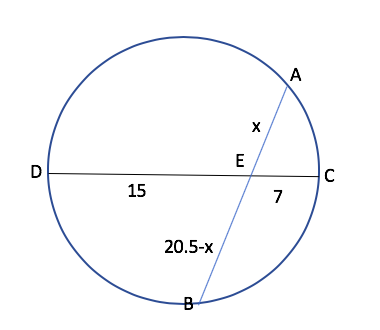
When two chords intersect inside a circle then  AE*BE=CE*DE

So x(20.5-x)=15*7

So x=10.5

So AE=10.5

BE=10

Difference in lengths=0.5

[/bg_collapse]

Q.15) The number of the real roots of the equation 2cos (x ( x + 1 ) ) = 2^x+ 2^-xis

a)Infinite

b)1

c)2

d)0

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)1[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Since in LHS we have cos theta whose value lies from -1 to 1

So LHS can have value from -2 to 2

RHS will always be >=2

since  2^x+2^-x =  (2^x) + (1/2^x)  and we know that sum of a number and its reciprocal is always greater than or equal to 2 if x is real using AM>=GM

So they intersect only once at x=0 when value of LHS and RHS is 2

So only 1 solution.

[/bg_collapse]

Q.16) 

a)3

b)6

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)3[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

f(2)=f(1)*f(1)

given f(1)=2

so f(2)=4

similarly f(4)=f(2)*f(2)=16…eqn 1

putting n=1 in given equation

f(a+1)=16

so we can say that a+1=4  …. from eq1

so a=3

[/bg_collapse]

Q.17) 

a)6144

b)6500

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)6144[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

a1=6

a1+a2=18

a2=12

a1+a2+a3=42

a3=24

a1+a2+a3+a4=90

a4=48

so a1, a2, a3, a4…an are in GP with ratio 2

so a11=a(2^10)=6(1024)=6144

[/bg_collapse]

Q.18) Amala, Bina, and Gouri invest money in the ratio 3 : 4 : 5 in fixed deposits having respective annual interest rates in the ratio 6 : 5 : 4. What is their total interest income (in Rs) after a year, if Bina’s interest income exceeds Amala’s by Rs 250?

*a)7250

b)6000

c)6350

d)7000

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)7250[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Let money invested be in ratio 300x:400x:500x

Bina’s interest income=400x*5*1/100

Amala’s interest income=300x*6*1/100

Difference=2x=250

X=125

Total interest income=20x+18x+20x=58x=58*125=7250

[/bg_collapse]

Q.19) AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to

a)9.1

b)9.3

c)7.8

d)8.5

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)9.1[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

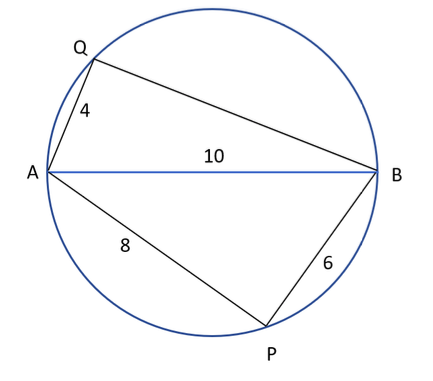
Angle AQB=90

Since angle in a semicircle is 90

So AQ^2+QB^2=AB^2

100=16+QB^2

QB=(84)^1/2=9.1 approx

[/bg_collapse] 

 

Q.20) Let S be the set of all points (x, y) in the x-y plane such that | x | + | y | ≤ 2 and | x | ≥ 1. Then, the area, in square units, of the region represented by S equals

a)2

b)8

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)2[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

 

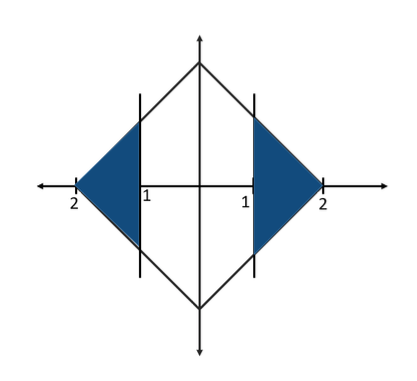
Here we have required area shaded in blue where we have 4 triangle having height=1 and base=1

So total area=4*(1/2 *1*1)=2 units 

[/bg_collapse]

Q.21) The product of the distinct roots of ∣x²− x − 6∣ = x + 2is

a)-8

b)-4

c)-16

d)-24

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]c)-16[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

|(x-3)(x+2)|=x+2

So x-3=1   or   x-3=-1

So x=4 or x=2

Also at x=-2 we have a solution so x=-2 is also a root

So product=2*4*-2=-16

[/bg_collapse]

Q.22)

a)5

b)10

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)5[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

|x| will be opened with +x or -x

‘so we get(-x)(6x^2+1)=5x^2

And x(6x^2+1)=5x^2

So for eq 1 we will have 3 solutions since it is cubic

For eq 2 we will have 3 solutions  since it is cubic

So 6 solutions

But x=0 will be a common solution so

Total=3+3-1=5 solutions

[/bg_collapse]

Q.23) For any positive integer n, let f(n) = n(n + 1) if n is even, and f(n) = n + 3 if n is odd.
If m is a positive integer such that 8f(m + 1) – f(m) = 2, then m equals

a)10

b)8

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)10[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

f(n) = n(n + 1) if n is even

f(n) = n + 3

Now, we don’t know that  if m is odd or even,

So lets take m is even, so value of (m+1) will be odd

Given 8f(m+1)-f(m)=2

So 8(m+1+3)-m(m+1)=2

m^2-7m-30=0

m=10, -3

but m must be positive as given in the question so m=-3 is not possible

so m=10

putting m=10 satisfies if you put it in the given function.

If m is odd, (m+1) will be even

So 8m(m+1)-(m+3)=2

8m^2+7m-5=0

m will come out as non integer.

[/bg_collapse]

Q.24) Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is

a)30

b)20

c)10

d)25

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)20[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Suppose first car starts 10:00 and it  travelled for 6 hour. Assume speed of car 1 is 10km/h. So in 6 hour it travelled 60km. Now car B will travel same distance in 5 hour so 60/5 =12km/h.

So, percentage change = 2/10*100 = 20%

Now If we take 7 hours instead of 6 hours  we get 60 /7 = 8.57

And for car 2 it will be 60/6 = 10km/h

So percentage change is less than 20%.

So at max it can be 20%

[/bg_collapse]

 

Q.25) A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is

a)45

b)43

c)38

d)32

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)43[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

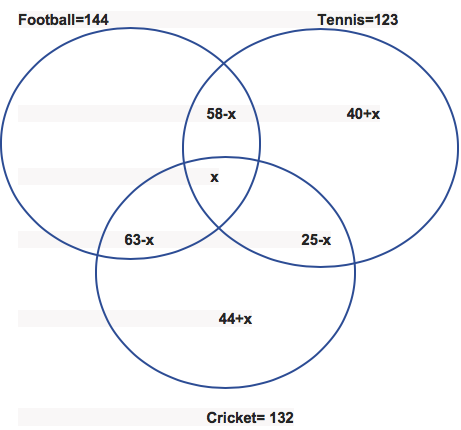
So, only football  144+109+x = 256

X=3

So. Only tennis = 40+x = 43

[/bg_collapse]

Q.26) In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse?

a)400

b)880

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)880[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

A beat B by 11 and A beat C by 90m. That means B is already 79m ahead of C. Now B will beat C by 80m and B is already 79m ahead so B will gain 1m lead in next 11m. So lead of 80 m will be in the span of 80*11= 880m 

[/bg_collapse]

Q.27) One can use three different transports which move at 10, 20, and 30 kmph, respectively. To reach from A to B, Amal took each mode of transport 1/3 of his total journey time, while Bimal took each mode of transport 1/3 of the total distance. The percentage by which Bimal’s travel time exceeds Amal’s travel time is nearest to

a)22

b)20

c)19

d)21

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)22[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

Let total distance = 60 km

So, Bimal will travel  1/3^rd  of total distance for each given speed

That means with the speed of 10 he will travel for 20 km = 2 hour

And with the speed of 20 km/h he will travel for 20 km = 1 hour

And with the speed of 30 km he will travel for 20 km =2/3 hour

So, total time = 3 hour 40 min = 220 min 

Now, for amal 1/3^rd of total travel time that means with the speed 20 it will travel for 1 hour, with the speed of 10 he will travel for 1 hour and with the speed of 30 it will travel of 1 hour.

So, total 3 hour=180 min

So, 40/180*100 =  22.22% = 22%

[/bg_collapse]

Q.28) A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is

a)80

b)85

c)75

d)70

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)80[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution: Liquid 1–1 lit = 1kg

Liquid 2—1 lit = 800 kg            5

Now 500 ml = 480 ml. so we need gap of 20ml,

And that gap will be made from liquid 2, if 1000ml = 800ml, so gap of 200 ml we need 1000ml,

20 ml gap can be achieved by 100 ml of liquid B

So, 400ml of liquid 1 is required.

400/500*100 = 80%

[/bg_collapse]

Q.29) The wheels of bicycles A and B have radii 30 cm and 40 cm, respectively. While traveling a certain distance, each wheel of A required 5000 more revolutions than each wheel of B. If bicycle B travelled this distance in 45 minutes, then its speed, in km per hour, was

a)16*pie

b)14*pie

c)18*pie

d)12*pie

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)16*pie[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

A travel 2*pie*r= 60*pie

B travel 2*pie*r = 80*pie

So lcm = 240*pie

That means A travel for 4 revolution and B travel for 3 revolution.

We need gap of 5000 revolution

So B will travel 5000*240*pie cm distance in 45 min

So speed  = 5000*240*pie/45 cm/min

To convert Cm into Km

1km =1000m and 1 m = 100 cm

So, 1km = 100000cm,

So 1cm = 10^-5 km

And 60 min = 1hour

So, speed = 5000*240*pie*60/45*100000 = 16*pie

[/bg_collapse]

 

Q.30) If the population of a town is p in the beginning of any year then it becomes 3+2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be

a) (1003)¹⁵ + 6

b) (997)2¹⁴ + 3

c) (1003)2¹⁵ – 3

d) (997)¹⁵ – 3

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]c) (1003)2¹⁵ – 3[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution: This is something we can do through options, as we know that from 2019 to 2034 there are 16 years including 2019 and 2034.

If we just make an equation and see how population in growing, we see it will be 1000,2003,4009,8021 and so on…

So, if we check option one by one 1003(2^0)-3 = 1000 for first year= 2019

For second year it will be 1003(2^1)-3 = 2003

For third year it will be 1003(2^2)-3 = 4009

So, option C will be the answer

[/bg_collapse]

Q.31) On selling a pen at 5% loss and a book at 15% gain, Karim gains Rs. 7. If he sells the pen at 5% gain and the book at 10% gain, he gains Rs. 13. What is the cost price of the book in Rupees?

a)40

b)80

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)80[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

X= price of pen

Y= price of book

So, 0.95x+1.15Y = x+y+7

-0.05x+0.15y = 7————(1)

 

1.05x+1.10y = x+y+13

0.05x+0.1y = 13————-(2)

 

Adding (1) and (2)

We get 0.25y =20

So, y=80

[/bg_collapse]

Q.32) If the rectangular faces of a brick have their diagonals in the ratio 3 : 2√3 : √15, then the ratio of the length of the shortest edge of the brick to that of its longest edge is

a)1: root3

b)2:root3

c)3:root3

d)none

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)1: root3[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution: Let A, B and C be the three diagonals.

So, a^2+b^2= 9

b^2+c^2=12

c^2+a^2=15

So, 2a^2+2b^2+2c^2=36

a^2+b^2+c^2 = 18

So, c^2=9, c=3

A=root6

B=root3

So, ratio of shortest to longest = 1: root3

[/bg_collapse]

Q.33) Let T be the triangle formed by the straight line 3x + 5y – 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is

a)9

b)15

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]a)9[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution: If we put x=0 we get Y=9

If we put Y=0  we get x=15

So points are (15,0), (0,9), (0,0)

And for right angle triangle circumradius is half of diameter

Here, diameter = 225+81= 306 = 17.49

So, radius = 17.49/2=8.74

So nearest integer will be 9

[/bg_collapse]

Q.34) With rectangular axes of coordinates, the number of paths from (1,1) to (8,10) via (4,6), where each step from any point (x, y) is either to (x, y+1) or to (x+1, y), is

a)3000

b)3920

[bg_collapse view=”button-blue” color=”#ffffff” expand_text=”Correct Answer” collapse_text=”Show Less” ]b)3920[/bg_collapse] [bg_collapse view=”button-orange” color=”#4a4949″ expand_text=”View Solution” collapse_text=”Show Less” ]

Solution:

We want to go to (1,1) to (8,10) through (4,6)

So, first we will go to (1,1) to (4,6) and then (4,6) to (8,10)

So from (1,1) to (4,6) we have 5+3 8 ways = 8!/5!3! =56
And from (4,6) to (8,10) we have 4 and 4 = 8 ways
So, 8!/4!4! = 70

So, total 56*70 = 3920 ways

[/bg_collapse]