Graph Implementation in C++ using Adjacency List and Matrix

Graphs are the most fundamental concept in data structures and in this blog we will be covering graph implementation in C++ using both adjacency matrix and adjacency list. In Graph, every node is connected with each other through edges that maintains the relationship between each other.

Graph is a hierarchical model that maintains network between nodes in a direct and undirected manner. There are different types of graph in data structure. So let us begin to understand the introduction and types of graph representation.

What is a Graph Data Structure?

Graphs are the important concept in computer science domain because it is worked on a hierarchical model. In Graph data structure there are two components that are nodes and edges where nodes are connected with each other through edges.

There are different types of graph in data structure which includes directed graph, undirected graph, weighted graph, cyclic graph, acyclic graph, complete graph, connected and disconnected graph.

Let’s understand graph easily through the visual representation which is given below in diagram. In this diagram A, B, C and D all are nodes connected through the edges and this is the example of undirected graph (consists of no direction).

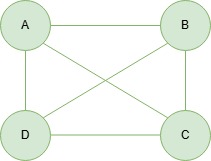
Types of Graphs Representation

There are two ways we can represent graphs :

1. Adjacency Matrix
2. Adjacency List

The first one is adjacency matrix in which we are showing relationship between vertices and edges. We are representing adjacency matrix through table format in that through rows we are representing the vertices and through column we are represents edges that connects vertices to each other.

Adjacency matrix comparatively represents the working of a mathematical concept “matrix” itself. In Matrix, entire field is consider to be a grid of rows and column and if we want to represent any element in a matrix then we can do so with the help of the rows and column number representation.

Let’s better understand the graph representation in C++ using both Adjacency Matrix and List in the next section.

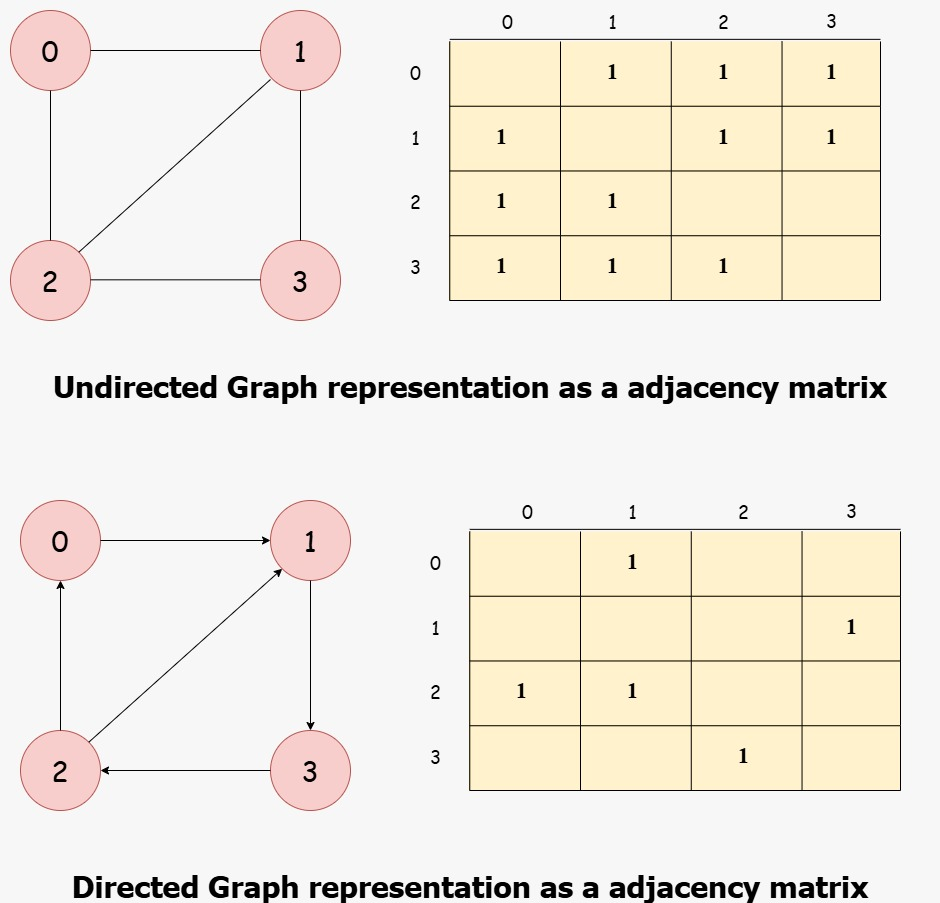
Graph Implementation in C++ using Adjacency Matrix

A graph can be represented in different ways. One of the simplest methods is using an adjacency matrix. This method is easy to understand and is ideal for dense graphs.

In an adjacency matrix, we use a 2D array where each cell shows whether there is a connection between two nodes. If there is an edge from node i to node j the matrix entry adj[i][j] is set to 1. If there is no edge it stays 0.

Here is a basic graph implementation in C++ using an adjacency matrix:

#include <iostream>
using namespace std;

class Graph {
private:
    int numVertices;
    int** adjMatrix;

public:
    Graph(int vertices) {
        numVertices = vertices;
        adjMatrix = new int*[numVertices];
        for (int i = 0; i < numVertices; i++) {
            adjMatrix[i] = new int[numVertices];
            for (int j = 0; j < numVertices; j++)
                adjMatrix[i][j] = 0;
        }
    }

    void addEdge(int i, int j) {
        adjMatrix[i][j] = 1;
        adjMatrix[j][i] = 1;
    }

    void removeEdge(int i, int j) {
        adjMatrix[i][j] = 0;
        adjMatrix[j][i] = 0;
    }

    void display() {
        for (int i = 0; i < numVertices; i++) {
            for (int j = 0; j < numVertices; j++) {
                cout << adjMatrix[i][j] << " ";
            }
            cout << endl;
        }
    }

    ~Graph() {
        for (int i = 0; i < numVertices; i++)
            delete[] adjMatrix[i];
        delete[] adjMatrix;
    }
};

int main() {
    Graph g(5);
    g.addEdge(0, 1);
    g.addEdge(0, 4);
    g.addEdge(1, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 3);
    g.addEdge(3, 4);

    cout << "Adjacency Matrix:" << endl;
    g.display();

    return 0;
}

This program creates a graph with 5 nodes and adds connections between them. The display function prints the adjacency matrix so you can easily see which nodes are connected.

Graph Implementation in C++ using Adjacency List

Another popular way to represent a graph data structure is using an adjacency list. This method is more memory efficient than an adjacency matrix especially when the graph is sparse.

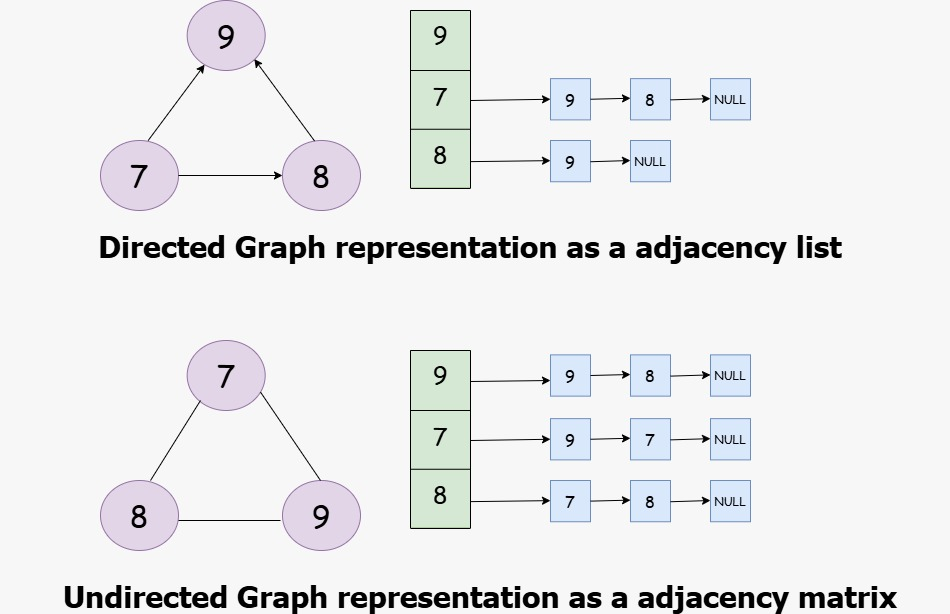
In an adjacency list each node stores a list of all the nodes that is connected to. This saves space because we only store edges that actually exist. Here is a simple graph implementation in C++ using an adjacency list:

#include <iostream>
#include <vector>
using namespace std;

class Graph {
private:
    int numVertices;
    vector<vector<int>> adjList;

public:
    Graph(int vertices) {
        numVertices = vertices;
        adjList.resize(numVertices);
    }

    void addEdge(int u, int v) {
        adjList[u].push_back(v);
        adjList[v].push_back(u);
    }

    void display() {
        for (int i = 0; i < numVertices; i++) {
            cout << i << ": ";
            for (int neighbor : adjList[i]) {
                cout << neighbor << " ";
            }
            cout << endl;
        }
    }
};

int main() {
    Graph g(5);
    g.addEdge(0, 1);
    g.addEdge(0, 4);
    g.addEdge(1, 2);
    g.addEdge(1, 3);
    g.addEdge(1, 4);
    g.addEdge(2, 3);
    g.addEdge(3, 4);

    cout << "Adjacency List:" << endl;
    g.display();

    return 0;
}

FAQs

What is the difference between adjacency matrix and adjacency list?

An adjacency matrix uses a 2D array to show all possible connections between nodes. An adjacency list uses linked lists or vectors to store only the existing edges. The list saves more memory when the graph has fewer edges.

Which is better for a large graph adjacency matrix or adjacency list?

For large graphs with fewer edges an adjacency list is better because it uses less memory.

Can I use the same code for directed graphs?

Yes you can use the same code for the directed graphs.