Heap Sort Algorithm (Complete Guide)

Heap Sort Algorithm is a sorting algorithm when we study trees. We have completed tutorial for most of the sorting algorithms like bubble sort, quick sort, merge sort, insertion sort, selection sort, radix sort, counting sort etc.

In this blog we will be covering almost every method for the heap tree construction whether it is adding elements one by one or heapify method. Understanding the concept of complete binary tree before walkthrough the heap sorting.

There are various steps involves in the creation of heap tree along with discussing the time and space complexity of heap tree data structure. It’s applications, advantages, disadvantages and the implementation of heap tree data structure in python programming language.

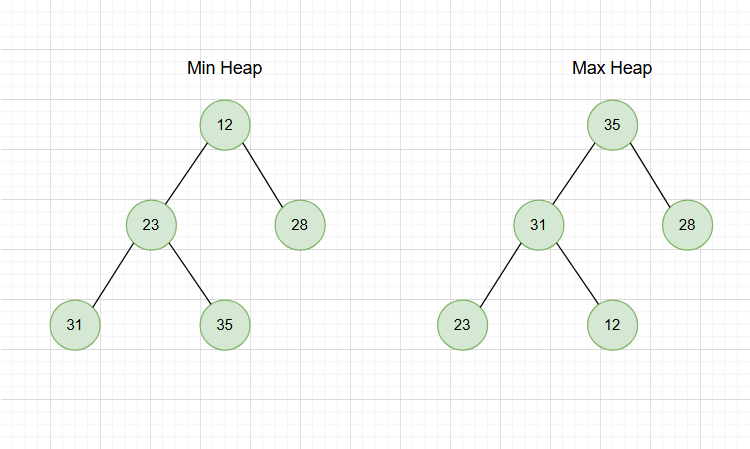
What is a heap tree data structure?

A heap tree data structure is a special type of complete binary tree data structure where the second last level of the entire tree is completely filled with nodes from left to right.

It satisfies the heapify along with follows the structural and ordering property. Heap tree is classified into two types which is min heap and max heap. In min heap, parent node value is less than the child node whereas in max heap the parent node value is greater than the child node.

If i will talk about the heap tree operations like insertion and deletion then i will add the nodes in a tree in such a way that the parent node should represent through variable ‘i’ and the addition of the left child in a tree is represented by ‘2i+1’ whereas the right child node of a tree is represented by ‘2i+2’.

What is heap sort algorithm?

Heap Sort Algorithm is a comparison-based sorting technique based on a Binary Heap data structure. It is similar to selection sort where we first find the maximum element and place it at the end. We repeat the same process for the remaining elements.

Key Concepts

• A binary heap is a complete binary tree which satisfies the heap property:
  • Max Heap: parent is greater than or equal to its children.
  • Min Heap: parent is less than or equal to its children.
• Heap sort uses a Max Heap to sort in ascending order.

Heap Sort Steps

1. Build a Max Heap from the input array.
2. Swap the root (maximum value) with the last element.
3. Reduce the heap size by one and heapify the root element.
4. Repeat the process until the heap size is 1.

def heapify(arr, n, i):
    largest = i          # Initialize largest as root
    left = 2 * i + 1      # left = 2*i + 1
    right = 2 * i + 2     # right = 2*i + 2

    # Check if left child is larger than root
    if left < n and arr[left] > arr[largest]:
        largest = left

    # Check if right child is larger than largest so far
    if right < n and arr[right] > arr[largest]:
        largest = right

    # Change root, if needed
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # swap

        # Heapify the root
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # Build max heap
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # Extract elements from heap
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # swap
        heapify(arr, i, 0)

# Example
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("Sorted array is:", arr)

Heap Tree Construction

Heap tree construction can be possible by using two ways which include the inserting of elements one by one and another way is the heapify method. The time complexity to do inserting elements one by one in a given order is O(n logn) whereas the complexity for the heapify method is O(n).

Insertion of elements one by one

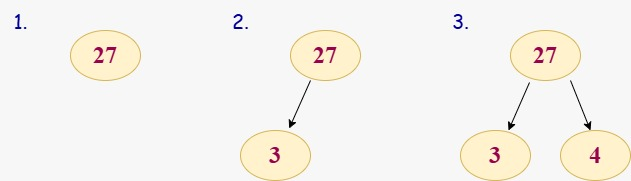
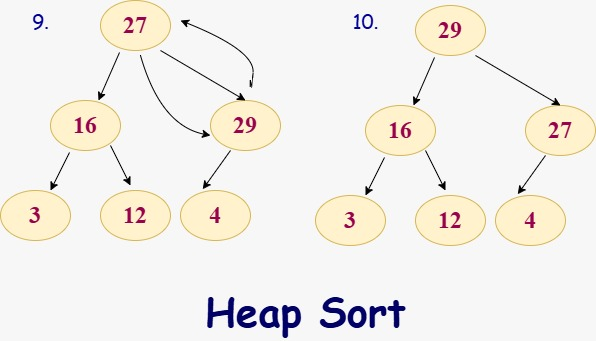
First step is to insert elements one by one as we have taken the array of elements [27, 3, 4, 12, 16, 29]. In the first diagram which is mentioned below we are first inserting 27 then 3 and at last 4. In this stage there is no need tp swap the element to satisfy the property as everything is aligned in the correct position.

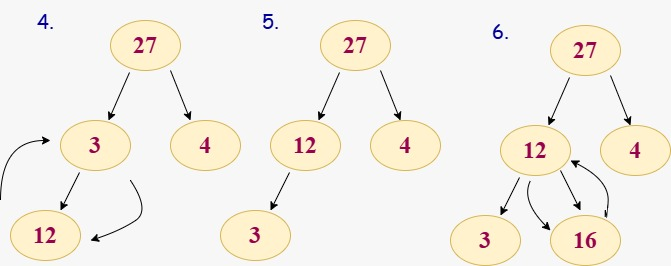
In the second, we have added 12 due to this property is not satisfied now then we have to swap the element 12 with 3 after making comparison, post adding 16 again we have to perform the swapping operation to satisfy the heap property.

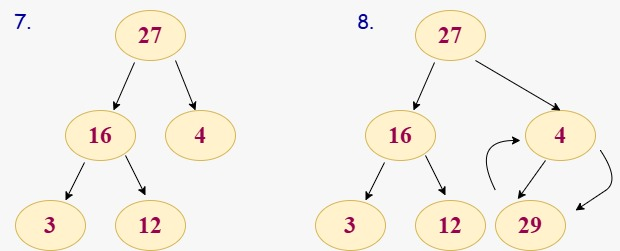
Post completing all 8 steps above now we are having 29 which is the largest element present in the array by using the comparison and swapping operation we have to fix that also and the final result is looking like this.

Heapify Method

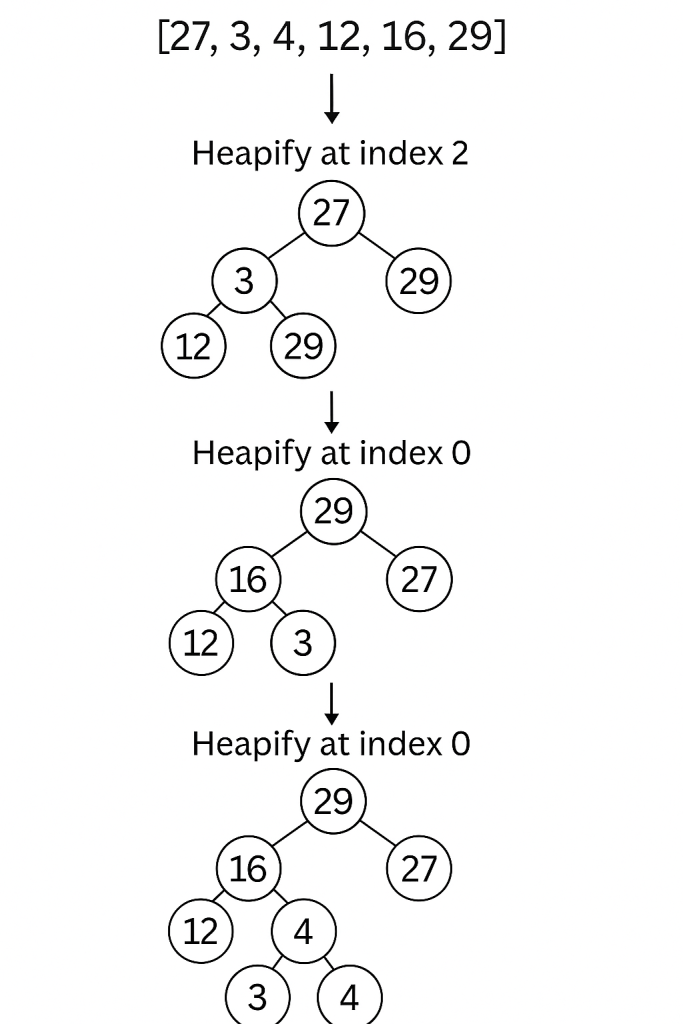
We begin from the last non-leaf node, which is at index n//2 – 1 = 6//2 – 1 = 2.
So we start heapifying from index 2 and move up to index 0.

Step 1: Heapify at index 2

• Subtree: Parent = 4 (index 2), Left = 29 (index 5), Right = None
• 29 > 4 → Swap them

Array becomes: [27, 3, 29, 12, 16, 4]

Step 2: Heapify at index 1

• Subtree: Parent = 3 (index 1), Left = 12 (index 3), Right = 16 (index 4)
• 16 > 3 → Swap them

Array becomes: [27, 16, 29, 12, 3, 4]

Step 3: Heapify at index 0

• Subtree: Parent = 27 (index 0), Left = 16 (index 1), Right = 29 (index 2)
• 29 > 27 → Swap them

Array becomes: [29, 16, 27, 12, 3, 4]

Now, the heap property is satisfied throughout the tree.

Implementation of heap sort algorithm

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:
        largest = left
    if right < n and arr[right] > arr[largest]:
        largest = right
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    for i in range(n - 1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("Sorted array is:", arr)

Advantages of Heap Sort Algorithm

1. Heap sort always runs in O(n log n) time, no matter what the input data looks like. This makes it reliable even for worst-case scenarios.
2. It sorts the data in place meaning it does not need extra memory or temporary arrays like merge sort does.
3. Because of its efficiency and low memory usage heap sort is a good choice for sorting large datasets.
4. Heap sort performs the same regardless of whether the input is already sorted, reverse sorted, or completely random.
5. Its consistent performance and non-recursive implementation make it suitable for systems where predictable execution time is important.

Disadvantages of heap sort algorithm

1. Heap sort is not a stable sorting algorithm which means it may change the relative order of equal elements during sorting.
2. Heap sort algorithm involves jumping around the array (due to the binary heap structure) which leads to inefficient use of the CPU cache and slower performance compared to quicksort in practice.
3. It tends to do more comparisons than other efficient sorting algorithms like quicksort or merge sort, which can make it slower for small or nearly sorted datasets.
4. The logic for maintaining the heap structure can be more difficult to implement and understand compared to simpler sorting methods like insertion sort or bubble sort.
5. Heap sort does not take advantage of existing order in the data. Even if the array is already partially sorted that means heap sort still performs the full sorting process without any performance gain.

Appplications of heap sort algorithm

1. Priority Queue Implementation
   Heap sort is commonly used in implementing priority queues. The max-heap or min-heap structure allows quick access to the highest or lowest priority element.
2. Job Scheduling Systems
   In CPU scheduling, heap sort helps in prioritizing tasks based on their deadlines or execution time. It ensures tasks are executed in the desired order efficiently.

1. Graph Algorithms
   Algorithms like Dijkstra’s shortest path and Prim’s minimum spanning tree use heaps to repeatedly select the next minimum-weight edge or vertex. This improves performance in large graphs.
2. Real-Time Event Simulation
   Heap sort can organize and manage future events based on their timestamps. Events are triggered in the correct sequence without delay.
3. Data Stream Handling
   When dealing with continuous data streams, heaps help in finding the top K largest or smallest elements on the fly. This is especially useful in analytics and monitoring systems.
4. Memory-Constrained Environments
   Since heap sort doesn’t require additional memory, it is suitable for embedded systems or environments with strict memory limits.

Know More About Heap Sort Algorithm

What is the time complexity for heap sort algorithm?

Best case: O(n log n)

Average case: O(n log n)

Worst case: O(n log n)

Is heap sort a stable sorting algorithm?

Heap sort is not stable. It may change the order of equal elements.

What is the space complexity of Heap Sort?

The space complexity of heap sort is O(1).

Is Heap Sort faster than Quick Sort?

Heap Sort has better worst-case performance but in practice Quick Sort is faster due to better cache usage and average case performance.