As we have came across multiple sorting algorithms like bubble sort, merge sort, quick sort, selection sort, insertion sort as well as counting sort. These all algorithms are categorized into two terms those are comparison based and non-comparison based algorithms.
In this blog we are covering another non-comparison based algorithm that is radix sort algorithm. This algorithm is based on the word that is ‘radix’ which means base or place value. We will cover it’s definition, advantages, disadvantages, complexity analysis and applications.
What is Radix Sort Algorithm?
Radix Sort Algorithm is a stable and non-comparison based algorithm. Radix sort is a sorting approach where we sort elements in an array according to the base digit of maximum element present in an array.
Radix Sort, Bucket Sort and Counting Sort all are the non-comparison based algorithms. Radix Sort will continue the process of sorting till all the elements are arranged in the correct position in an array. Let’s explore the working of radix sort algorithm in detail.
Here is a basic example to understand this algorithm
To sort [170, 45, 75, 90, 802, 24, 2, 66], Radix Sort will be like this
- Sort by units place: [170, 90, 802, 2, 24, 45, 75, 66]
- Then by tens place: [802, 2, 24, 45, 66, 170, 75, 90]
- Finally by hundreds place: [2, 24, 45, 66, 75, 90, 170, 802]
Working of Radix Sort Algorithm
In this section we will talk about the working of radix sort algorithm step by step in a detailed manner :
Normalize Element Lengths
This is the first step where we apply radix sort on each element to made them equal in length by padding zeroes in the beginning of the element like this :
| 804 | 804 |
| 5 | 005 |
| 79 | 079 |
| 690 | 690 |
| 7 | 007 |
Sort By Digits (Right to Left)
Next step post appending zero before starting of each elements is to sort the elements by digits in order from right to left. There are different passes are there in this step to sort the digits.
Pass 1: Sort by Units Place (Rightmost Digit)
| Number | Units Digit |
| 804 | 4 |
| 5 | 5 |
| 79 | 9 |
| 690 | 0 |
| 7 | 7 |
Sorted by units digit
| Sorted Order |
| 690 |
| 804 |
| 5 |
| 7 |
| 79 |
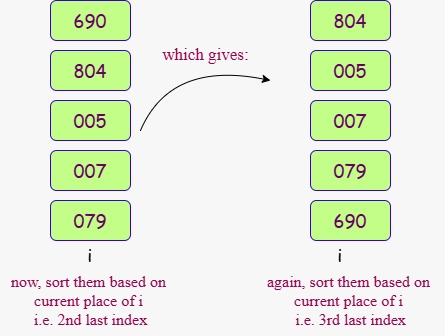
Pass 2: Sort by Tens Place
| Number | Tens Digit |
| 690 | 9 |
| 804 | 0 |
| 5 | 0 |
| 7 | 0 |
| 79 | 7 |
Sorted by tens digit (stable sort)
| Sorted Order |
| 804 |
| 5 |
| 7 |
| 79 |
| 690 |
Pass 3: Sort by Hundreds Place
| Number | Hundreds Digit |
| 804 | 8 |
| 5 | 0 |
| 7 | 0 |
| 79 | 0 |
| 690 | 6 |
Sorted by hundreds digit
| Sorted Order |
| 5 |
| 7 |
| 79 |
| 690 |
| 804 |
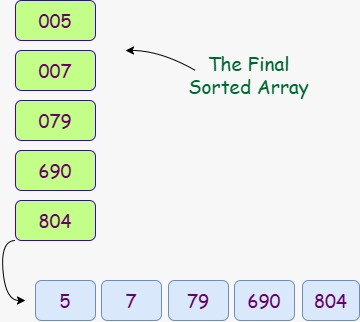
Final Sorted Array
Post sorted by unit digit places we got our sorted array using radix sort
Implementation of Radix Sort Algorithm in Python
Radix Sort is a way to sort numbers by looking at each digit one by one and starting from the rightmost digit (units place) to the leftmost digit. In Python we can do this by grouping the numbers based on each digit using a list of buckets like 0 to 9 and repeating this for every digit place. This method works best for numbers and is very fast when the numbers are not too large.
def counting_sort(arr, place):
size = len(arr)
output = [0] * size
count = [0] * 10
# Count occurrences
for num in arr:
digit = (num // place) % 10
count[digit] += 1
# Cumulative count
for i in range(1, 10):
count[i] += count[i - 1]
# Build the output array
i = size - 1
while i >= 0:
digit = (arr[i] // place) % 10
output[count[digit] - 1] = arr[i]
count[digit] -= 1
i -= 1
# Copy to original array
for i in range(size):
arr[i] = output[i]
def radix_sort(arr):
max_num = max(arr)
place = 1
while max_num // place > 0:
counting_sort(arr, place)
place *= 10
# Example usage
arr = [804, 5, 79, 690, 7]
radix_sort(arr)
print("Sorted array:", arr)
Time Complexity of Radix Sort
Table 1 shows the time and space complexity of radix sort algorithm that is O(n * k) where n is the number of elements present in an array and k is the number of passes in the algorithm to sort the elements in an array.
| Case | Time Complexity |
| Best Case | O(n × k) |
| Average Case | O(n × k) |
| Worst Case | O(n × k) |
| Space | O(n + k) |
| Stable | Yes |
| Comparison-based | No |
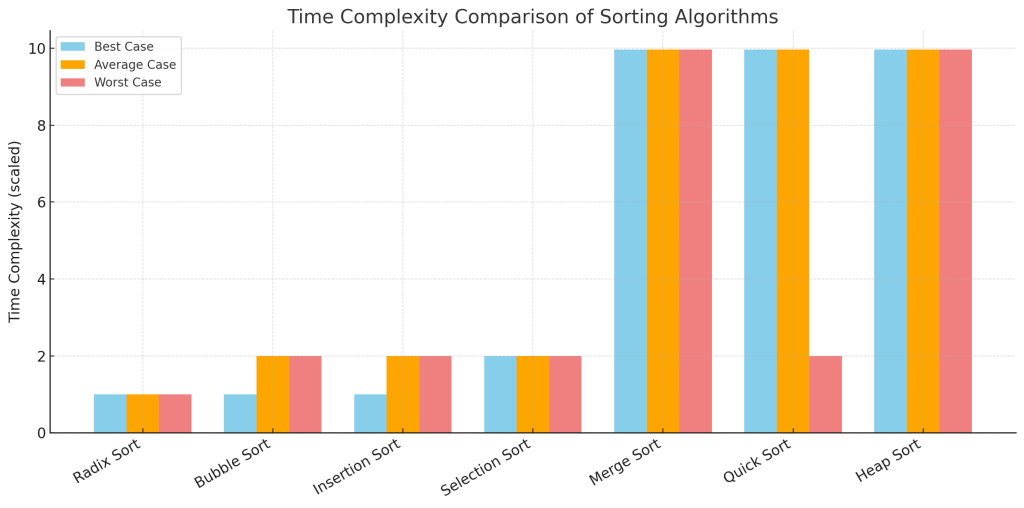
In this table we are comparing radix sort time complexity in all the cases whether it is best case, average case or worst case with other algorithms. Along with comparing the space complexities too.
| Algorithm | Best Case | Average Case | Worst Case | Space Complexity | Stable |
| Radix Sort | O(n × k) | O(n × k) | O(n × k) | O(n + k) | Yes |
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) | Yes |
| Insertion Sort | O(n) | O(n²) | O(n²) | O(1) | Yes |
| Selection Sort | O(n²) | O(n²) | O(n²) | O(1) | No |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) | No |
| Heap Sort | O(n log n) | O(n log n) | O(n log n) | O(1) | No |
Advantages of Radix Sort
- Radix Sort can achieve linear time O(nk) when the number of digits (k) is small relative to the input size which is making it faster than comparison-based sorts like QuickSort for large datasets.
- It maintains the relative order of equal elements which is essential when sorting complex records based on multiple keys.
- Especially useful for sorting strings, phone numbers, or IDs where the number of digits and characters are limited.
- Radix Sort Algorithm performs well on large datasets.
Disadvantages of Radix Sort
- Radix Sort requires extra space for counting and bucketing which makes it less space-efficient compared to in-place sorting algorithms.
- It is not suitable for sorting floating-point numbers or negative numbers without significant modifications to the algorithm.
- The performance of Radix Sort heavily depends on the number of digits k so it may become inefficient when k is large.
- It is less flexible than comparison-based sorts since it only works efficiently with fixed-length or uniformly formatted data.
- Radix Sort can be slower than QuickSort or Merge Sort for small datasets due to its overhead in digit wise processing and bucket management.
Applications of Radix Sort
- Radix Sort is commonly used when dealing with large datasets of integers particularly when the number of digits is relatively small. In such cases, it can outperform comparison-based algorithms by providing near-linear time complexity.
- Finally, Radix Sort plays a vital role in text processing and string matching tasks like suffix array construction. These applications benefit from Radix Sort’s ability to handle large volumes of substrings or suffixes efficiently and stably.
Know More About Radix Sort Algorithm
What type of data is Radix Sort best suited for?
Radix Sort works best with numbers or words that have a fixed length, like phone numbers, zip codes, or ID numbers.
Is Radix Sort faster than QuickSort?
The answer is yes radix sort is working faster with the large number of datasets in comparison with quick sort.
Is Radix Sort a stable sorting?
Yes the radix sort is a stable sorting algorithm because when it comes to sort the elements in radix sort this factor comes in the picture.
Where is radix sort used in real life ?
Radix Sort is used to sort things like phone numbers, ID cards and in some other systems that work with digital data or text.